trójkąt matura: W trójkącie ABC na bokach AB i AC obrano odpowiednio punkty M i N tak,że |AM| : |AB|=1:4 i |CN|=3|AN| Proste DM i BN przecinają się w punkcie K Wyznacz stosunek pola czworokąta AMKN do pola trójkąta CBK

matura: przepraszam za błędny wpis miało być proste CM i BN

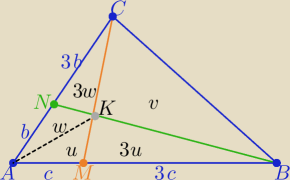
Eta: w,u, v −− wartości odpowiednich pól w ΔACM i BCM : 3(4w+u)=v+3u ⇒ v=12w w ΔABN i BCN : 3(4u+w)=3w+v ⇒ v=12u to u=w P(AMKN)=w+u=2u P(BKC)=v=12u

P(AMKN)		1
	=
P(BKC)		6

============