To jest dla mnie za trudne zad. ostrosłup prawidł. czworokątny... Renata z III a: W ostrosłupie prawidłowym czworokątnym wysokość wynosi 5, a kąt dwuścienny przy podstawie ma 120 stopni. Oblicz objętość. To jest zadanie z matur, za 6 pkt. To mój ulubiony dział, ale zadanie za trudne. Bardzo proszę o chociaż plan w punktach.

xyz: nie rozumiem wyrażenia "kąt dwuścienny przy podstawie" czy chodzi o kąt między dwiema sąsiednimi ścianami bocznymi? bo w ostrosłupie prawidłowym kąt dwuścienny między podstawą i ścianą boczną z całą pewnością jest ostry

Jerzy: Przcinasz bryłe płaszczyzną prostopadłą do krawędzi bocznej i przechodzącą przez przekątną podstawy.Przekrojem jest trójkąt równoramienny o kącie wierzchołkowym 120.Potem korzystasz z podobieństwa trójkątów.Próbuj.

Renata z III a: Do xyz: oczywiście chodzi o kąt między sąsiednimi ścianami bocznymi. Jerzy: rysunek mam, ale nie wiem, które trójkąty są podobne. Z proporcją nie miałabym kłopotu, ale gapię się na rysunek i nie wiem które trójkąty wybrać.

Jerzy: @xys, treść mętna,ale kąt między podstawą a ścianą nie może być rozwarty.

Jerzy: @Renata, narysuj przkrój przez wierzchołek i drugą przekątną.

Renata z III a: Jerzy, no tak, mętnie piszę... To jest kąt między ścianami, tylko tak jakby na dole narysowany, nie potrafię się wysłowić:( Jerzy, mam już ten przekrój od wierzchołka zawierający krawędzie boczne i przekątną podstawy. I które trójkąty są podobne?

Jerzy: Zaraz ktoś zrobi ci rysunek.W przekroju dostaniesz dwa położone na sobie trójkąty prostokątne, gdze krótszą przyprostokątną mniejszego jest bok trójkąta , ktory jest przekrojem bryły ( odcinek prostopadły do krawędzi na tym rysunku).

Jerzy: Nie narysuję telefonem

Xyz: Można bez podobieństwa, ale wtedy jest bardzo dużo liczenia Też raczej nie narysuję i nie napiszę lewą ręką. Prawą mam złamaną.

Renata z III a: A ja z kolei nie mogę dołączyć swego rysunku Zaczekam ile trzeba, nawet do wieczora

Xyz: a − krawędź podstawy b − krawędź boczna H= 5 h₁² = (a/2)²+25 b² = (a√2/2)²+25 a*h₁ = b*h₂ (a√2)² = h₂²+h₂² − 2h₂*h₂*cos 120 Z tego można wyliczyć a, ale to jest dość koszmarne

Renata z III a: Przyjmujemy, że h1 to wys. ściany bocznej tak? I ostatnia linia to tw. cosinusów. I byłby układ równań z 3 niewiadomymi ?

Xyz: A może nie tak bardzo 2a² =3h₂² I będzie a²*(a²+100)/4 = (a²+50)*2a²/6 Dalej łatwo o ile się nie pomyliłam bo wszystko liczę w pamięci. Pisać jeszcze nie mogę.

Xyz: h₁ wysokość ściany bocznej opuszczona na a h₂1 wysokość ściany bocznej opuszczona na b i oczywiście bok tego przekroju

Renata z III a: Wszystko zapisałam i będę analizowała krok po kroczku. Zad. za 6 pkt są kosmiczne. Xyz bardzo Ci dziękuję i życzę pogodnego spędzania świąt. Jesteś wielka

Xyz: Dobrych świąt 😊

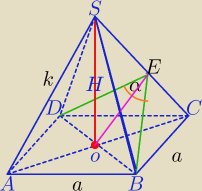
Mila: α=120^o,H=5 OE⊥SC 1) w ΔBOE:

	OB
tg60o=
	OE

|OB|=|OE|√3, |OC|=|OB| 2)

	1		5		5
PΔSOC=		|OC|*H=		|OC|=		*|OE|*√3
	2		2		2

	1
PΔSOC=		k*|OE|
	2

Porównanie:

5		1
	*|OE|*√3=		k*|OE|⇔k=5√3
2		2

3) W ΔSOC: H²+|OC|²=k² 5²+|OC|²=(5√3)² |OC|²=75−25 |OC|=√50=5√2 2|OC|=10√2

	1
PABCD=		*(10√2)2=100
	2

4)

	1
V=		*100*5
	3

	500
V=		[j3]
	3

===============