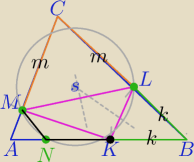
oo ix: Na bokach AB , BC i CA trójkąta ABC wybrano odpowiednio punkty K, L i M w ten sposób, że |BK | = |BL | i |CL | = |CM|. Okrąg opisany na trójkącie KLM przecina bok AB tego trójkąta w punkcie N takim, że |AN | < |AK|. Udowodnij, że |AN|=|AM|.

Mila:

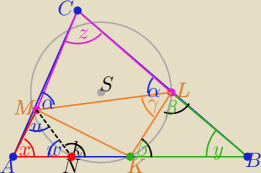
Eta: ∡y=180^o−2β , ∡z=180^o−2α to ∡x= 2α+2β−180^o ∡α+γ+β=180^o ⇒γ=180^o−(α+β) czworokąt NKLM jest wpisany w okrąg z warunku wpisania czworokąta w okrąg : ∡ k =α+β to ∡w= 180^o−(α+β) =γ to ∡u= 180^o−x −γ = 180^o−2α−2β+180^o − 180⁺α+β=180^o−(α+β)= γ zatem ∡u=∡w więc ΔANM jest równoramienny czyli |AN|=|AM| ============== c.n.w.