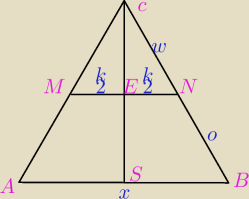
planimetria Mo: Hej W trójkącie równoramiennym ABC, w którym |AC|=|BC|, podstawa |AB|=x. Na ramionach AC i BC tego trójkąta wybrano odpowiednio punkty M i N w taki sposób, że MN || AB i |MN| = (|AM|+|BM|)/3. Przyjmując, że kąt MNB=α wyznacz długość |MN| w zależności od x i od kąta α. Moje pytanie: czy ma ktoś może odpowiedź do tego zadania, albo dla rozrywki chce sobie policzyć? W skrócie: ja skorzystałam raz z twierdzenia sinusów dla trójkąta ENC, by wyznaczyć "w", a następnie z podobieństwa ΔSBC ~ ΔENC. Mój wynik: |MN| = ^x_1−3cosα Jako "k" oznaczam odcinek |MN|, jako "o" oznaczam ³₂k (z informacji podanej z tresci zadania). Pozdrawiam i miłego wieczoru chętnym.

Mo: odświeżam

Mo: Dla chętnych w przyszłości − ten wynik jest poprawny.