dowodzenie RubikSon: Udowodnij, ze jeżeli suma odległości dowolnego punktu trójkąta ostrokątnego od jego boków jest równa długości jednej z wysokości trójkąta, to trójkąt ten jest równoboczny.

RubikSon: Odświeżam

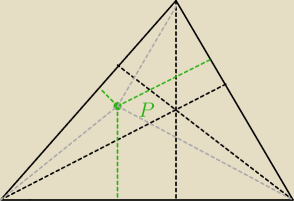
wredulus_pospolitus: Zauważ, że jeżeli z punktu P poprowadzimy odcinki do wierzchołków trójkąta ABC, to otrzymamy trzy trójkąty. suma pól tych trzech trójkątów równa jest polu trójkąta ABC dodatkowo 'odległości' punktu P od boków są niczym innym jak wysokościami tych mniejszych trójkątów. załóżmy, że H₁ + H₂ + H₃ = h_AB

	|AB|*hAB		|AB|*(H1+H2+H3)
PABC =		=
	2		2

a więc mamy:

|AB|*(H1+H2+H3)		|AB|*H1 + |BC|*H2 + |AC|*H3
	=		⇔
2		2

H₂(|AB| − |BC|) + H₃(|AB| − |AC|) = 0 i tutaj należy zauważyć, że to równanie ma być spełnione dla DOWOLNEGO POŁOŻENIA punktu P ... czyli H₂ i H₃ przyjmują (w miarę) dowolne wartości (tak aby spełniać warunek: H₁ + H₂ + H₃ = h_AB), tak więc − powyższe równanie będzie ZAWSZE spełnione jedynie gdy |AB| = |BC| oraz |AB| = |AC|

Mila: