nierówności pomocy lolpo: Witam mam takie zadanie : Rozwiąż nierówność (x−2)(x+3)<0 Ze wzoru skróconego mnożenia wychodzi mi oczywiście, że miejscami zerowymi są : 2 i −3. Jednak gdy chcę to zrobić deltą wymnażam sobie nawiasy, wychodzi mi x²−5x+6<0 po podstawieniu do wzoru na x1 i x2 wychodzi : −5+1/2 = −3 −5−1/2 = −2 Dlaczego to się nie zgadza?

lolpo: Poprawka : −5+1/2= −2 −5−1/2 = −3

)): (x−2)(x+3)= x²+x−6

lolpo: Już rozumiem. To nie będzie jednak w ten sposób, x²−x−6<0? x*x daje x²+2x−3x−6? Zmieniłem znaki i 2x−3x daje −1. −2*3 daje −6. Jeśli jest w ten sposób czyli x²−x−6 to po podstawieniu −x czyli −1 pod b we wzorze na deltę wyjdzie b² czyli −1² da 1. Jeśli nie to skąd ten plus jeśli ma wyjść x²+x−6?

Bleee: −2x + 3x

lolpo: Ok dziękuję. Drugie pytanie jest takie iż robię te nierówności razem z matemaksem i przykładowo mam nierówność typu x²−x−2<0 Liczę deltę i wychodzi x1 = −1−3/2=−2 x2= −1+3/2=1 Według wzoru tam zawsze jest −b+pierwiastek z delty i −b−pierwiastek z delty. Natomiast jemu wychodzi x1 = 1−3/2=1 i x2 = 1+3/2=2 Chodzi mi o to, że nie stawia − przed liczbą podstawioną pod b i wtedy wychodzi na odwrót. Czy mój wynik jest zły?

ABC: x²−x−2<0 ⇒ b=−1 ⇒ −b=1

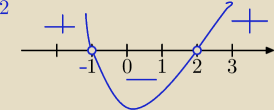
Mila: Rozwiąż nierówność (x−2)(x+3)<0 1) deltę liczysz , aby trójmian przedstawić w postaci iloczynowej. W zadaniu masz już postać iloczynową i nie ma potrzeby liczyć Δ. Liczysz miejsca zerowe: x−2=0 lub x+3=0 x=2 lub x=−3 Widzisz na pewno , że po wymnożeniu przy x² otrzymasz wsp. a=1 >0 Zatem masz parabolę skierowana do góry Rozwiązanie nierówności : x∊(−3,2) 2) x²−x−2<0 − parabola skierowana do góry a=1, b=−1 , c=−2 Chcemy przedstawić wyrażenie w postaci iloczynowej: Δ=9

	1−3		1+3
x1=		lub x2=
	2		2

x₁=−1 lub x₂=2 (x+1)*(x−2)<0 x∊(−1,2)

lolpo: Czyli jeśli b=−1 to −b=1 więc jeśli b=1 to −b=−1?

Mila: −(−1)=1 −(−2)=2 −(−6)=6