g
dambyldor: Na bokach AB ,BC ,CD i DA czworokąta ABCD wybrano punkty K ,L,M i N takie, że
| AK | | BL | | CM | | DN | |
| = |
| = |
| = |
| = k,gdzie k ∈ (0,+ ∞ ). |
| KB | | LC | | MD | | NA | |
Oblicz stosunek pola czworokąta KLMN do pola czworokąta ABCD .
15 kwi 14:43
wredulus_pospolitus:
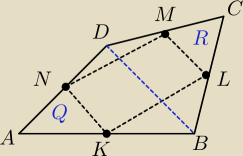
Zauważ, że:
1) ΔAKN jest podobny do ΔABD
2) ΔCML jest podobny do ΔCDB
| | 1 | |
co więcej, znamy skalę podobieństwa ... stąd wiemy, że Q = PANK = |
| PADB, |
| | 4 | |
| | 1 | |
analogicznie R = |
| PCDB |
| | 4 | |
| | 1 | | 1 | |
Czyli Q+R = |
| (PADB + PCDB) = |
| PABCD |
| | 4 | | 4 | |
analogicznie postępujesz z ΔBKL i ΔDNM i co otrzymujesz

15 kwi 14:56
wredulus_pospolitus:
PS. zastanów się skąd wiemy, że ów trójkąty są podobne <−−− to jest klucz do zadania
15 kwi 14:57
ite:
| | 1 | |
wredulus a jak rozwiązać gdy skala podobieństwa wynosi np. |
| ? |
| | 4 | |
15 kwi 15:34
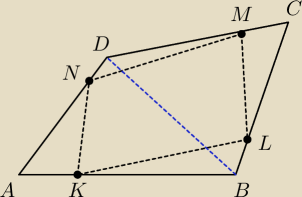
 Zauważ, że:
1) ΔAKN jest podobny do ΔABD
2) ΔCML jest podobny do ΔCDB
Zauważ, że:
1) ΔAKN jest podobny do ΔABD
2) ΔCML jest podobny do ΔCDB

