funkcja homograficzna maciek: O pewnej funkcji homograficznej danej wzorem ^a_x−p+q wiadomo, że jej wykres rośnie gdy x ∈ (−∞,−1) ∪ (−1,+∞), zbiorem wartości jest R − {1} oraz do wykresu należy punkt (−2,3). a. Wyznacz wzór funkcji oraz sporządź jej wykres. b. Dla jakich argumentów x funkcja przyjmuje wartości niedodatnie. c. Rozwiąż nierówność f(x) > f(x+1). d. Dla jakiej wartości parametru k, równanie f(x) = ^2−k_k−1 nie ma rozwiązań? Proszę o pomoc

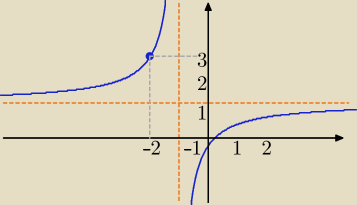
iteRacj@: −rysunek poglądowy− Czy na pewno był taki zapis (−∞,−1) ∪ (−1,+∞) ? Dalej spróbuj sam to rozwiązać.

maciek: o matko, dziękuję bardzo tak, dokładnie taki zapis

iteRacj@: Tam nie może być znak U.

maciek: no to nie wiem, pewnie chodziło o spójnik i,ale tak jest w zadaniu asymptota pionowa: −1 to p, asymptota pozioma: 1 to q czyli jak f(−2) = 3 to 3 = ^a₋₂₋₁−1 czyli ^a₋₃= 4, więc a=−12 wzór funkcji to ⁻¹²_x−1−1 czyli −^11+x_x−1 nierówność: −^11+x_x−1>−^11+(x+1)_(x+1)−1 prawdziwa dla przedziału <0,1> z parametrem k wyszedł mi brak rozwiązań, więc chyba coś źle. nie jestem pewny czy jest dobrze, mógłby ktoś sprawdzić? będę bardzo wzdzięczny

iteRacj@:

	2−k
d/ Musisz rozwiązać równanie		=1 (to jedyna wartość jakiej nie przyjmuje funkcja
	k−1

f(x)) .

iteRacj@: p=−1 więc x−p=x+1

iteRacj@: Dobrze napisałeś: asymptota pionowa → −1=p, asymptota pozioma → 1=q, ale do wzoru źle podstawiłeś. Musisz poprawić wzór funkcji f(x).