Znajdź równanie prostej równoległej do prostej Drake: Znajdź równanie prostej równoległej do prostej o równaniu 3y+2x−4=0 przechodzącej przez punkt A=(a,b), gdzie a<b, zaś liczby a i b są pierwiastkami równania |cos⁴x−sin⁴x|=¹_√2 należącymi do przedziału <0,π>.

Jerzy: Wskazówka: | |= |cos2α |

janek191:

	1
I cos4 x − sin4 x I = I ( cos2 x + sin2 x)*( coa2 x − sin2 x) I =
	√2

	√2
I cos2 x − sin2 x I =
	2

	√2
I cos 2 x I =
	2

	√2		√2
cos 2 x =		lub cos 2 x = −
	2		2

	π		3
2 x =		lub 2 x =		π
	4		4

	π		3
x =		lub x =		π
	8		8

Dokończ

Drake: Ale co mam zrobić z tym ^π₈ i ³₈π, czy to są współrzędne punktu które mam postawić?

Drake: ?

janek191:

	π		3
A = (		,		π )
	8		8

kasia0948: Mam pytanie odnośnie tego zadania, mianowicie mamy tak:

	1
|cos2x|=		, zatem mamy:
	√2

	π
x=		+kπ
	8

	7π
x=		+kπ
	8

	3π
x=		+kπ
	8

	5
x=		+kπ
	8

	π		kπ
zatem: x=x=		+
	8		4

kasia0948: Przypadkiem kliknelam wyslij, ale dalej mamy tak:

	π		3π		5π		7π
x∊{		,		,		,		}
	8		8		8		8

Zatem możliwe punkty A to:

	π		3π		π		5π		3π		5π
A={(		,		),(		,		),(		,		),
	8		8		8		8		8		8

	π		7π		3π		7π		5π		7π
(		,		),(		,		),(		,		)}
	8		8		8		8		8		8

Gdzie popełniam zatem błąd?

Mila:

4 2
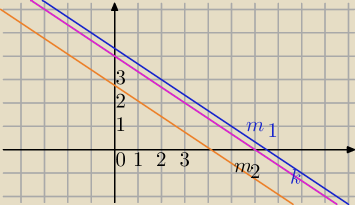
	=6 i masz 6 punktów, zatem będzie 6 prostych równoległych do danej prostej:

k: 2x+3y−4=0

	π		3π		π		3π
m1 : 2*(x−		)+3*(y−		)=0 gdzie (		,		)∊m1
	8		8		8		8

	11π
2x+3y−		=0
	8

	π		5π
m2: (		,		)∊m2
	8		8

	π		5π
2*(x−		)+3*(y−		)=0
	8		8

itd

kasia0948: Aha, ja myślałam, że za dużo tych prostych i popełniam błąd, ale to najwidoczniej janek191 popełnił, dziękuję Mila za sprostowanie moich myśli