. pomocy: w graniastoslupie podstawa jest kwadratem o boku dlugosci 2. przekatne scian bocznych tworza kat o mierze 30 stopni. oblicz pole powierzchni calkowitej tego graniastoslupa

Jerzy: Oblicz drugi bok prostokąta, którego jeden bok to 2, a przkątne tworzą kąt 30

Leszek: Sa to zapewne przekatne sasiednich scian bocznych wychodzace z jednego wierzcholka ? ? Wowczas z twierdzenia cosinusow : (2√2)² = x² + x{2} − 2x cos 30° x − przekatna sciany bocznej , nastepnie drugi bok sciany bocznej z tw.Pitagorasa !

Jerzy: Nie jest powiedziane „przekątne sąsiednich ścian bocznych”.

Leszek: Czesc Jerzy , nie ma tego w tresci zadania , ale uczniowie czesto wpisuja fragmenty tresci , wiec tylko tak podpowiedzialem taka wersje zadania , niech uczen zrobi , taka wersja jaka podalem jest dosc czesto w zbiorach zadan maturalnych o profilu podstawowym !

pomocy: jest to zadanie z rozszerzenia, i napisałem całe zadanie bez pominiętego żadnego fragmentu

Leszek: Tak , w profilu podstawowym nie ma tw.cosinusow

pomocy: jak wykorzystac to tw cosinusów? bo nie wiem /

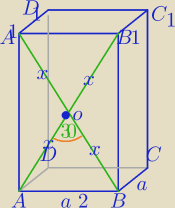
Mila: 1) W ΔAOB: 2²=x²+x²−2x*x cos30^o

	√3
4=2x2−2x2*		⇔4=2x2−x2√3
	2

x²*(2−√3)=4 /*(2+√3) ⇔x²*(4−3)=4*(2+√3) x²=4*(2+√3) 2)

	|AB1|*|BA1|		2x*2x		1
PABB1A1=		*sin30o=		*
	2		2		2

P_ABB1A1=x²=4*(2+√3) 3) P_c=2*2²+4*4*(2+√3)=8+16(2+√3) dokończ