prostokąt
matma3:
Dany jest prostokąt ABCD o obwodzie 28, wiedząc,że pole koła wpisanego
w trójkąt ABD jest równe 4π Oblicz pole prostokąta i podaj długości jego boków
13 kwi 18:16
janek191:
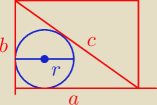
2 a + 2 b = 28
a + b = 14
b = 14 − a
r = 0,5*(a + b − c)
π r
2 = 4 π
r = 2
====
więc
2 = 0,5*( 14 − c)
4 = 14 − c
c = 10
=====
a
2 + b
2 = c
2
a
2 + ( 14 − a)
2 = 100
a
2 + 196 − 28 a + a
2 − 100 = 0
2 a
2 − 28 a + 96 = 0 / : 2
a
2 − 14 a + 48 = 0
( a − 6)*(a − 8) = 0
a = 6 lub a = 8
więc
b = 14 − 6 = 8 lub b = 14 − 8 = 6
Odp. P = 48 j
2
===============
13 kwi 18:31
Eta:
Dołożę swoje "trzy grosze"

a+b=14 i r=2
z tw. o odcinkach stycznych
|BD|= a−2+b−2= 14=4=10
a
2+b
2=d
2 ⇒ (a+b)
2−2ab=100 ⇒ 14
2−100=2ab ⇒ ab=48=P
=========
a+b=14 i ab=48 ( ze wzorów Viete
'a) ⇒ a=6 i b=8 lub a=8 i b=6
=====================
13 kwi 18:42
Eta:
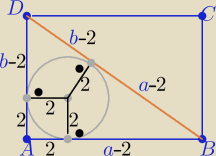
13 kwi 18:48
 2 a + 2 b = 28
a + b = 14
b = 14 − a
r = 0,5*(a + b − c)
π r2 = 4 π
r = 2
====
więc
2 = 0,5*( 14 − c)
4 = 14 − c
c = 10
=====
a2 + b2 = c2
a2 + ( 14 − a)2 = 100
a2 + 196 − 28 a + a2 − 100 = 0
2 a2 − 28 a + 96 = 0 / : 2
a2 − 14 a + 48 = 0
( a − 6)*(a − 8) = 0
a = 6 lub a = 8
więc
b = 14 − 6 = 8 lub b = 14 − 8 = 6
Odp. P = 48 j2
===============
2 a + 2 b = 28
a + b = 14
b = 14 − a
r = 0,5*(a + b − c)
π r2 = 4 π
r = 2
====
więc
2 = 0,5*( 14 − c)
4 = 14 − c
c = 10
=====
a2 + b2 = c2
a2 + ( 14 − a)2 = 100
a2 + 196 − 28 a + a2 − 100 = 0
2 a2 − 28 a + 96 = 0 / : 2
a2 − 14 a + 48 = 0
( a − 6)*(a − 8) = 0
a = 6 lub a = 8
więc
b = 14 − 6 = 8 lub b = 14 − 8 = 6
Odp. P = 48 j2
===============
 a+b=14 i r=2
z tw. o odcinkach stycznych
|BD|= a−2+b−2= 14=4=10
a2+b2=d2 ⇒ (a+b)2−2ab=100 ⇒ 142−100=2ab ⇒ ab=48=P
=========
a+b=14 i ab=48 ( ze wzorów Viete'a) ⇒ a=6 i b=8 lub a=8 i b=6
=====================
a+b=14 i r=2
z tw. o odcinkach stycznych
|BD|= a−2+b−2= 14=4=10
a2+b2=d2 ⇒ (a+b)2−2ab=100 ⇒ 142−100=2ab ⇒ ab=48=P
=========
a+b=14 i ab=48 ( ze wzorów Viete'a) ⇒ a=6 i b=8 lub a=8 i b=6
=====================
