wzory viete'a
salv: Oblicz sume kwadratów pierwiastków równania 3x
4−12x
2+5=0.
t=x
2
3t
2−12t+5=0
t
12+t
22=(t
1+t
2)
2−2t
1t
2
t
1+t
2=4
| | 38 | |
t12+t22=(t1+t2)2−2t1t2= |
| |
| | 3 | |
| | 38 | |
x12+x22=√(t12+t22)=√ |
| |
| | 3 | |
Mógłby ktoś sprawdzić ?
13 kwi 12:56
6latek: A ile tych pierwiastkow bedzie ?
13 kwi 13:04
Jerzy:
| | 38 | |
To co policzyłeś,: |
| , to suma kwadratów kwdratów pierwiastków, a polecenie w zadaniu |
| | 3 | |
jest inne.
13 kwi 13:09
PW:
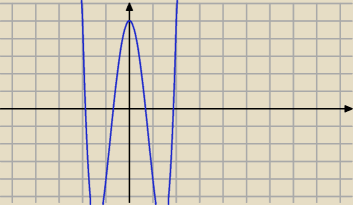
Jak widać − są 4
rozwiązania równania.
Wynika to np. z parzystości funkcji x
4−12x
2+5 (są 2 dodatnie, to muszą być również 2 ujemne).
13 kwi 13:13
Mila:
x
2=t, t>0
3t
2−12t+5=0
Δ=144−3*4*5=84
| | 12−2√21 | | 12+2√21 | |
t1= |
| >0 lub t2= |
| >0 |
| | 6 | | 6 | |
x
1=
√t1 lub x
2=−
√t1 lub x
3=
√t2 lub x
4=−
√t22
x
12+x
22+x
32+x
42=2t
1+2t
2=2*(t
1+t
2)=2*4=8
14 kwi 22:16
Mila:
x4=−√t2
14 kwi 22:37
Eta:
Funkcja jest parzysta Δ>0
ze wzorów Viete
'a
to suma kwadratów wszystkich pierwiastków jest równa
8
14 kwi 22:57