d czikita: Na bokach AB , AD i BC rombu ABCD wybrano odpowiednio punkty K,L i M w ten sposób, że odcinki KL i KM są równoległe do przekątnych rombu. Wykaż, że odcinek LM przechodzi przez punkt przecięcia przekątnych rombu.

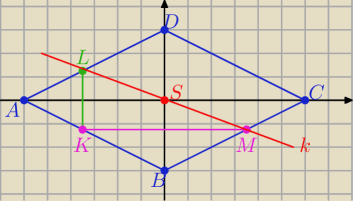
Eta: 1 ze sposobów analitycznie Umieszczam romb w układzie współrzędnych tak jak na rys. S(0,0) , L(−x, y) i M((x, −y) współczynnik kierunkowy prostej LM

	−y−y		−y
a=		⇒ a=		⇒ y=ax
	x+x		x

to LM : y=ax i S(0,0) należy do tej prostej co kończy dowód

czikita: dzięki za pomoc a jakbys jeszcze mogla zrobic to jeszcze innym sposobem, to bylby bardzo wdzieczny

Eta: 2 sposób ΔKLM jest prostokątny to środek okręgu opisany na tym trójkącie pokrywa się ze środkiem S odcinka LM

czikita: Czyli okrąg wpisany w romb, będzie miał rzecz jasna środek w S, a okrąg opisany na trójkącie prostokątnym, to będzie ten sam okrąg, tak? I stąd wiemy, że S będzie w połowie przeciwprostokątnej. ?