W graniastosłupie prawidłowym trójkątnym wysokość podstawy ma długość Kaskada: W graniastosłupie prawidłowym trójkątnym wysokość podstawy ma długość 4√3. Cosinus kąta zawartego między przekątnymi dwóch sąsiednich ścian bocznych , które wychodzą z tego samego wierzchołka jest równy ⁸₉. Oblicz pole całkowite graniastosłupa.

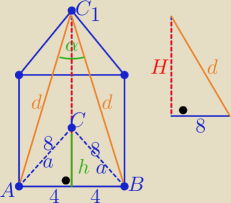
Eta: h_p=4√3 to a=8 .......... z tw. cosinusów w ΔABC₁

	d2+d2−82		32		8
cosα=		⇒ 1−		=		⇒ d2=..........
	2*d*d		d2		9

H²=d²−a² ⇒H=............

	1
Pc=2*		*a*hp + 3aH= ..................
	2

Highway137: Eta co to jest za twierdzenie cosinusów?

Jerzy: https://pl.wikipedia.org/wiki/Twierdzenie_cosinus%C3%B3w

Highway137: Jerzy który to jest dokładnie wzór?

Jerzy: Ten pierwszy.

Highway137: Jak tam w żadnym wzorze nie ma kreski ułamkowej

6latek: tak miedzy nami .O co Tobie sie rozchodzi?

Jerzy: Bo we wzorze cosinusów nie ma kreski ułamkowej.

Highway137: To o co chodzi z tym cosα=^d2+d2−82_2*d*d ?

Jerzy: Dla trójkąta ABC₁ możemy zapisać: (4 + 4)² = d² + d² − 2*d*d*cosα, i teraz oblicz z tego wzoru cosα