Podzieliłem wysokość ostrosłupa na 6 i jakiś x i nie wiem co dalej Konrad: W kulę o promieniu 6 wpisano ostrosłup prawidłowy trójkątny tak, że środek kuli znajduje się wewnątrz ostrosłupa. Jaka powinna być wysokość tego ostrosłupa, aby jego objętość była największa. Podaj tę objętość

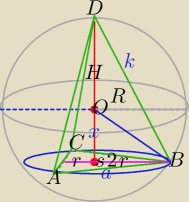
Mila: R=6, |OS|=x, |DS|=H,0<H<12 H=x+6, x=H−6

	2		a√3		a2
(H−6)2+(		*		)2=36⇔H2−12H+36+		=36
	3		2		3

	a2
H2−12H+		=0
	3

a²=3*(12H−H²) =============

	1		a2√3
V=		*		*H
	3		4

	(12H−H2)		1
V(H)=		*H=		*(12H2−H3)
	4		4

	1
V'(H)=		*(24H−3H2)
	4

V'(H)=0⇔24H−3H²=0 ⇔3H*(8−H)=0 H=8 ( uzasadnij, że dla H=8 jest maksimum) a²=3*(12*8−64)=3*32=96 a=4√6

	1		3*32√3
V=		*		*8
	3		4

V_max=64√3 =========== To jest czworościan foremny ! Sprawdź dł. krawędzi, jest równa 4√6

Konrad: Dziękuję