1 zadanko
1 zadanie: Wyznacz resztę z dzielenia liczby 32018 przez 16.
11 kwi 20:31
Adamm:
φ(16) = φ(24) = 23*(2−1) = 8
2018 ≡ 2 (mod 8)
z tw. Eulera
32018 ≡ 32 = 9 (mod 16)
reszta to 9
11 kwi 20:33
Maciess:
3
0=1 mod 16 =1
3
1=3 mod 16 =3
3
2=9 mod 16 =9
3
3=27 mod 16=11
3
4=81 mod 16=1
3
5=243 mod 16=3
przypuszczam, że dalej będzie sie powtarzać reszta 1,3,9,11 więc mozna w ten sposob cos
wykombinowac
11 kwi 20:39
Maciess:
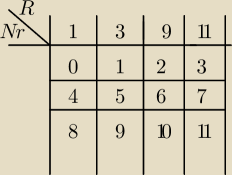
Nie wiem z jakirego poziomu to zadanie więc wrzuce swoje prymitywne rozwiązanie.
R to reszta, nr to wykładnik
Sprawdzamy do którego z 4 ciągów arytmetycznych nalezy 2018.
0+4(n−1)=2018
n∉ℕ nie nalezy
2+4(n−1)=2018
n=502
należy do tego ciągu więc reszta z dzielenia to 9
11 kwi 20:56
jc:
34 ≡ 1 (mod 16)
2018 ≡ 2 (mod 4)
Dlatego 32018 ≡ 32 (mod 16)
czyli reszta = 9
11 kwi 21:27
11 kwi 21:29
1 zadanie: Dzięki
11 kwi 21:32
Maciess: Z ciekawości na jakim etapie nauki pojawiają sie takie zadania? Czy to jakieś konkursy, zadania
ze szkoły sredniej/gimnazjum?
11 kwi 22:03
Adamm:
Myślę że
1. Konkursy
2. Studia
Szkoła średnia? Hmm... w sumie nie wiem.
11 kwi 22:08
1 zadanie: Zadanie ze szkoły średniej
11 kwi 22:34
Maciess: czyli moj prymitywny sposób adekwatny do poziomu. Chociaż nie wiem jaki jest poziom w innych
szkołach, ze swoją lepiej nie będę porównywał.
11 kwi 22:38
jc: Maciess, zauważyłeś cykl o długości 4 i zaraz potem wykorzystałeś znajdując prawidłową
odpowiedź. Zrobiłem dokładnie to samo, tylko nieco inaczej zapisałem.
11 kwi 23:14
an: 3
2018=3
2016*9=(3
2016−1)*9+9
| (32016−1)*9+9 | | (31008−1)*(31008+1)*9+9 | |
| = |
| ...... |
| 16 | | 16 | |
2016=2*2*2*2*2*63
Czyli reszta 9 przez 16 , a także przez 32
Nie znam programów, ale to raczej spokojnie mieści się w gimnazjum
12 kwi 00:59
an: ta reszta 9 będzie dla2n przy 4 ≤ n ≤ ciekawe ile nie chce mi się bawić,
ale wygląda że grubo ponad 20
12 kwi 01:40