oblicz objętość wika: Podstawą ostrosłupa jest trójkąt równoramienny o ramionach długości b i kącie między nimi α . Wszystkie krawędzie boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem β. Wyznacz objętość ostrosłupa. odp: V= ^{b3*sinα*tgβ}_{12cos u α/2}

Eta:

	1
Pp=		b2*sinα
	2

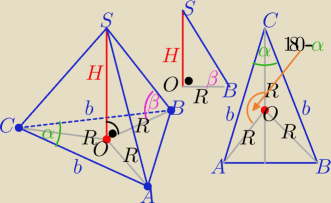
Spodek wysokości pokrywa się ze środkiem okręgu o promieniu R opisanego na podstawie z tw. cosinusów w ΔAOC b²=R²+R²−2R*R*cos(180^o−α) , cos(180^o−α)= −cosα b²=2R²(1+cosα) , 1+cosα= 2cos²(α/2) to R²= U{b²}{4cos²(α/2)

	b
R=
	2cos(α/2)

Z tw. Pitagorasa w ΔOBS H= R*tgβ =..............

	1
V=		Pp*H =.......................
	3

co daje:

	b3sinα*tgβ
Odp : V=
	12cos(α/2)

=================

wika: dziękuję bardzo