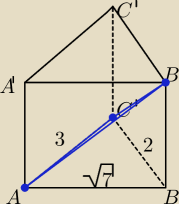
mono Maciess: Graniastosłup prosty trójkątny o bokach 2,√7,3. Płaszczyzna przechodzi przez najdłuższy bok podstawy i jeden z wierzchołków drugiej podstawy. Otrzymane przekrój jest trojkątem o polu 3√3 Oblicz cosinus kąta między między ramionami tego trojkąta oraz cosinus między płaszczyzną przekroju a płaszczyzną podstawy. Moze rysunek nie za piękny ale cos widac. Mam pole przekroju więc policzyłem jego wysokość. Problem raczej z pierwszą częścią zadania.

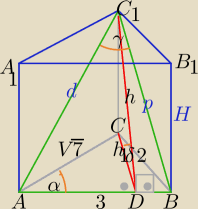
Mila: 2<√7<3 1) P_ΔABC1=3√3

1
	*3*h=3√3
2

h=2√3 2) Pole ΔABC : 2²=√7²+3²−2*3*√7cosα

	2		√3
cosα=		, sinα=
	√7		√7

	1		√3		3√3
PΔABC=		*3*√7*		=
	2		√7		2

3√3		1
	=		*3*h1
2		2

h₁=√3 ======

	√3		1
3) cosδ=		=		⇔δ=60o ( i to bardzo ułatwia resztę)
	2√3		2

dalej sam

janek191: 3) cos δ dobrze policzone ?

janek191: Dobrze

Maciess: Dało rade. Próbowałem zrobić pierwszą część zadania, a tak naprawdę trzeba było od tyłu. Wielkie dzięki wyniki sie zgadzają

Maciess:

	5√13
cosγ=
	26

Mila:

Mila: To jak jest w Twojej szkole, oceny maturzystom wystawiono?

Maciess: Oceny właśnie dziś wszystkie zostały w e−dzienniku uzupełnione. Ale nie wiadomo co z klasyfikacją. Rozmawiałem dzis z naczucielami w szkole (cała szkoła strajkuje) i mówią ze sami nie wiedzą co będzie. Z jednej strony nie chcą przerywać strajku, a z drugiej nie chcą też nam problemów robić. Wszystko sie wyjasni na dniach.

Mila: To dobrze, że oceny wystawione. Myślę, że będą konferencje klasyfikacyjne.