Wyznacz wartości parametru. Marcin: Wyznacz wartości parametru m, dla których równanie x³+(m−1)x−m=0 ma dokładnie dwa różne pierwiastki rzeczywiste.

Jerzy: Tam ma być x³ ?

jc: Przecież jest. x³+(m−1)x−m=(x−1)(x²−x−m) m=0 lub m=−1/4

jc: Szukamy m, dla którego wielomian x²−x−m ma pierwiastek podwójny lub ma dwa różne pierwiastki, z których jeden jest równy 1. Dla m=−1/4 mamy dwa rozwiązania: 1, 1/2. Dla m=0 mamy dwa rozwiązania: 1, 0.

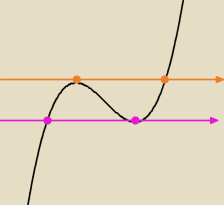ite: jc czy graficznie to ma być jedna z tych sytuacji?

jc: Tak, jeden pierwiastek podwójny, a jeden pojedynczy.

ite: jc dziękuje za wyjaśnienie