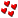całki, całki Majma:

	dx
∫
	11   1+3sinxcosx− cos2x   y

Proszę o zrobienie tego przykładu od A do Z z wytłumaczeniem co i jak i dlaczego Chciałabym to zrozumieć w końcu raz, a dobrze. Dziękuję!

Bleee: A ten y to co tam robi,

Bleee: 1 = sin²x + cos²x I coś przeczuwam wzór skróconego mnożenia w mianowniku

ICSP: 1. sin²x + cos²x = 1 2. Wyciągasz cos²x w mianowniku przed nawias 3. Stosujesz podstawienie t = tg(x) 4. Całka została sprowadzona do całki z funkcji wymiernej. 5. Stosujesz metody pozwalające liczyć całki z funkcji wymiernych.

Majma: @Blee własnie nie mam pojęcia :') Możemy założyć, że wykładowcy chodziło o 4, ale ja still widzę "y"

Majma: Nie wychodzi mi nadal. Moglibyście pokazać?

Mariusz:

	dx
∫
	11   cos2x+sin2x+3sinxcosx− cos2x   y

	dx
∫
	11   sin2x+3sinxcosx+(1− )cos2x   y

	1	dx
∫
	11   tg2x+3tgx+1−   y	cos2x

t = tgx

	dx
dt =
	cos2x

	dt
∫		=
	11   t2+3t+1−   y

	dt
∫
	3   5   11   (t+ )2− −   2   4   y

	dt
∫
	3   5   11   (t+ )2−( + )   2   4   y

Teraz musisz rozważyć trzy przypadki 1.

5		11
	+		< 0
4		y

2.

5		11
	+		= 0
4		y

3.

5		11
	+		> 0
4		y

W dwóch pierwszych przypadkach odpowiedź możesz zapisać od razu W trzecim przypadku przydatny będzie rozkład na sumę ułamków prostych chyba że znasz funkcje hiperboliczne i do nich odwrotne