logarytmy olete: oblicz dla jakich wartości α liczby tg²α, tg³α, tg³α + tgα+1 w podanej kolejności są wyrazami ciągu arytmetycznego ogarnąłem że r=tgα+1 i r=tg³α−tg²α czyli tgα+1=tg³α−tg²α ⇒ tg³α−tg²α−tgα−1=0 podstawiłem tgα za t i wychodzi t³−t²−t−1=0 i dalej nie wiem co... Hornerem mi nie wychodzi, tak samo jak parowaniem, czy moglibyście mi powiedzieć co robię źle?

ABC: dobrze przepisałeś treść?

mat: a może geometrycznego?

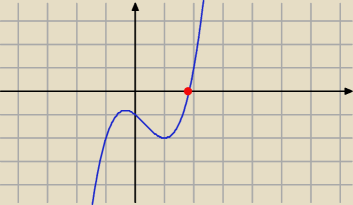
PW: Rozwiązanie istnieje. Jeżeli umiesz znaleźć tę liczbę t₀, to odpowiedź będzie α = arctg(t₀). Nie jest to zadanie dla licealisty.

ABC: PW , Mariusz miałby raczej odmienne zdanie w tej kwestii

PW: Tak, wiem, on to rozwiąże. Ja nigdy się tego nie nauczyłem (to znaczy wiem o co idzie, ale bez zaglądania do wzorów nie rozwiążę, i dobrze mi z tym).

olete: treść jest dobrze

ABC: jesteś w szkole średniej czy na studiach?

Mariusz: ABC oczywiście Vax był gimnazjalistą gdy mu pokazałem sposób rozwiązywania równań trzeciego i czwartego stopnia Wzory skróconego mnożenia i rozwiązywanie układów równań za pomocą podstawiania są za trudne dla licealisty ? No nieźle się poziom obniżył W przypadku trzech rozwiązań rzeczywistych przydatna jest też trygonometria i wiadomości o funkcjach w tym o funkcji odwrotnej

ABC: akurat Vaxa obserwowałem parę lat temu na matematyka.pl i on nie był zwyczajnym gimnazjalistą , taki się trafia 1 na 1000 mniej więcej

Mariusz: olete przypomnij wzory skróconego mnożenia na sześcian sumy i różnicy kwadrat sumy i różnicy różnicę kwadratów Wspomniałeś schemat Hornera Możesz go użyć do przedstawienia wielomianu w postaci sumy potęg dwumianu tak aby wyrugować wyraz z x² Gdy przyjrzysz się wzorom skróconego mnożenia to będziesz wiedział jak dobrać wyraz wolny tego dwumianu Schemat Hornera oczywiście stosujesz kilkukrotnie

PW: olete, odpowiedz na pytanie: Jesteś licealistą czy studentem? bo szkoda czasu.

Mariusz: Przedstawiasz wielomian w postaci sumy potęg dwumianu tak aby wyrugować wyraz z x² Zakładasz że rozwiązanie jest w postaci sumy dwóch składników Gdy zastosujesz wzór na sześcian sumy zauważysz że z środkowych wyrazów możesz wyciągnąć wspólny czynnik Wstawiasz przewidywaną postać rozwiązania do równania i grupujesz wyrazy Zapisujesz równanie w postaci układu równań Jeżeli znasz wzory Vieta możesz równanie kwadratowe zapisać od razu a jeżeli nie rozwiązujesz układ metodą podstawiania Do rozwiązania równania kwadratowego wzory skróconego mnożenia też mogą być przydatne najpierw wzór na kwadrat sumy bądź różnicy a później na różnicę kwadratów

Mariusz: PW gdyby był studentem to by miał zbiór zadań Krysickiego i Włodarskiego i tam miałby sposób podany , skrótowo bez wyprowadzania ale wiedziałby przynajmniej jak rozwiązywać takie równanie W zbiorze tym są jeszcze trzy przykłady użycia tych wzorów

olete: dobra, skleiłem, dzięki wielkie

olete: I jestem w liceum

Mariusz: Ja uważam że można licealiście pokazać sposób na równanie trzeciego i czwartego stopnia nie wykraczający poza to co miał w programie nauczania Zespolone trzeba wtedy zastąpić trygonometrią Nie będzie to może sposób stricte algebraiczny ale korzystając z zespolonych i tak dostalibyśmy rozwiązanie w postaci funkcyj trygonometrycznych gdybyśmy chcieli oddzielić część rzeczywistą od części urojonej t³−t²−t−1=0 Chcemy przedstawić wielomian w postaci sumy potęg dwumianu tak aby pozbyć się wyrazu z t² Ze wzorów skróconego mnożenia wiemy że (a−b)³=a³−3a²b+3ab²−b³

	1
Przyjmując a = t nasze b musi być równe
	3

t³−t²−t−1=0

	1		1		1		1
(t−		)3=(t3−3		t2+3		t−		)
	3		3		9		27

	1		1		1
(t−		)3=(t3 − t2 +		t −		)
	3		3		27

1
	+c=−1
3

	4
c=−
	3

	1		4		1		1		1		4		1
(t−		)3 −		(t−		)=(t3 − t2 +		t −		) −		(t−		)
	3		3		3		3		27		3		3

	1		4		1		11
(t−		)3 −		(t−		)=t3 − t2 − t +
	3		3		3		27

11
	+d=−1
27

	11
d=−1−
	27

	38
d = −
	27

	1		4		1		38
(t−		)3 −		(t−		) −		= t3 − t2 − t − 1
	3		3		3		27

Ze wzorów skróconego mnożenia wiemy że (a + b)³ = a³+3a²b+3ab²+b³ Zauważmy że ze środkowych wyrazów możemy wyciągnąć wspólny czynnik i zmienić kolejność składników (a + b)³ = a³+b³+3ab(a+b) Zauważmy że wzór ten przypomina postać równania więc może dobrym pomysłem byłoby założenie że rozwiązanie jest postaci y = u + v

	1		4		1		38
(t−		)3 −		(t−		) −		= 0
	3		3		3		27

	1
Niech y = t−
	3

mamy wówczas równanie

	4		38
y3 −		y −		= 0
	3		27

Załóżmy że rozwiązanie jest postaci y = u + v zatem

	4		38
u3+v3+3uv(u+v) −		(u+v) −		= 0
	3		27

	38		4
u3 + v3 −		+ 3(u+v)(uv−		)=0
	27		9

Zapisujemy powyższe równanie w postaci układu równań

	38
u3 + v3 −		=0
	27

	4
3(u+v)(uv−		)=0
	9

Dlaczego w ten sposób ? Zauważ że w drugim równaniu mamy iloczyn a iloczyn jest równy zero gdy co najmniej jeden z czynników jest równy zero Zauważ ponadto że w drugim równaniu jeden z czynników jest równy u+v ale wcześniej przyjęliśmy że y=u+v więc nie możemy tego czynnika przyrównać do zera

	38
u3 + v3 =
	27

	4
(uv−		)=0
	9

	38
u3 + v3 =
	27

	4
uv=
	9

	38
u3 + v3 =
	27

	64
u3v3=
	729

Powyższy układ równań to wzory Vieta dla równania kwadratowego o pierwiastkach u³ oraz v³

	38		64
z2 −		z +		= 0
	27		729

	19		361		64
(z −		)2−		+		= 0
	27		729		729

	19		297
(z −		)2 −		= 0
	27		729

	19 − 3√33		19 + 3√33
(z −		)(z −		) =0
	27		27

	1
u+v =		(3√19 − 3√33+3√19 + 3√33)
	3

	1		1
t−		=		(3√19 − 3√33+3√19 + 3√33)
	3		3

	1
t =		(3√19 − 3√33+3√19 + 3√33 + 1)
	3

Możesz tę metodę uogólnić na czwarty stopień Różnice Pozbywasz się wyrazu z t³ Zakładasz że rozwiązanie jest w postaci sumy trzech składników Układ równań który dostaniesz będzie wzorami Vieta dla równania trzeciego stopnia Na forum o którym wspomniał ABC spotkałem się też z innym sposobem na równanie trzeciego stopnia Przyjmujesz że wielomian trzeciego stopnia jest w postaci sumy bądź różnicy dwóch sześcianów dwumianów liniowych Sposób ten po uogólnieniu na czwarty stopień wymaga nieco mniej obliczeń

Bartek: