Ostrosłup prawidłowy. nick1: Punkt S jest wierzchołkiem ostrosłupa prawidłowego czworokątnego, a punkty E, F są odpowiednio środkami krawędzi AB i CD jego podstawy. Krawędź podstawy i wysokość tego ostrosłupa mają taką samą długość równą 1. Płaszczyzna przechodząca przez punkty E i F przecina krawędzie boczne odpowiednio w punktach G oraz H. Oblicz pole otrzymanego przekroju, wiedząc, że jest ono dwa razy większe od pola czworokąta BCGH. Będę bardzo wdzięczny za dokładne wytłumaczenie.

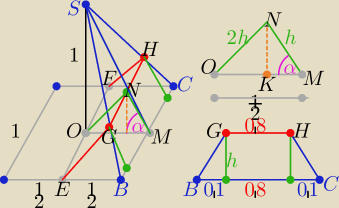
Eta: Przekrojem jest trapez równoramienny EFHG Trapezy EFHG i BCHG mają podstawy równej długości i wysokości 2h i h ( bo pola są w stosunku 2:1 z treści zadania W ΔSOM tgα= |SO|/|OM| ⇒ tgα=2 to cosα=1/√5 z tw. kosinusów w ΔOMN 4h²=h²+¹₄−2*h*¹₂*¹_√5 to 3h²+¹_√5h−¹₄=0 Δ=16/5 , √Δ=4/√5 to h=1/2√5 więc 2h= 1/√5 oraz w ΔOMN cosα=|KM|/h ⇒ |KM|=1/10 to |OK|=9/10 to |GH|=0,8 oraz |BC|=1 i h=1/2√5 więc P(EFHG)=2P(BCHG) = 2* (¹₂*1,8*¹_2√5)=^1,8√5₁₀ P(EFHG)=0,18√5 ================ Ciekawe czy taką masz odp? Ładne zadanko

nick1: Odpowiedź się zgadza. Ślicznie dziękuje!