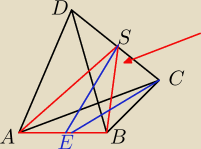
Stereometria asd: Dany jest ostrosłup prawidłowy trójkątny, w którym długość krawędzi podstawy jest równa a . Kąt między krawędzią boczną i krawędzią podstawy ma miarę 4 5∘ . Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju. Zadanie zrobiłem,ale jak sprawdzić w innych tego typu zadaniach,czy BS pada pod kątem prostym do DC,albo czy kąt CSE jest prosty?

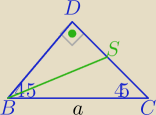
Mila: To zależy od danych. Suma kątów w trójkącie lub twierdzenie odwrotne do tw. Pitagorasa lub tw. cosinusów, podobieństwo,... W tym przypadku |∡BDC|=90^o. BS jest środkową poprowadzoną do przyprostokątnej, patrz rysunek. Wniosek?