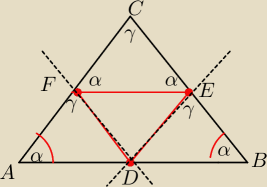
trojkat rownoramienny 6latek: Udowodnij ze trojkat ktorego wirzcholkami sa srodki bokow trojkata rownoramiennego jest tez trojkatem rownoramiennym Pomyslaem nad wykorzystaniem kątow czyli dwie proste rownolegle przeciete sieczna (kąty odpowiadajace Stad mam rowne katy przy podsatwie FE stad wniosek z etrojkat jest rownoramienyy Drugi pomysl to poprowadzic dwusieczna kata γ i tez wykazac przystawanie trojkatow (mialbym prostokatne Jest jakis jeszce inny ?

Mila: |AC|=|BC|

	1
FE||AB, |FE|=		|AB|
	2

	1
FD||BC, |FD|=		|BC|
	2

	1
DE||AC, |DE|=		|AC|
	2

Wniosek?

6latek: Dobry wieczor Milu Wiesz to jest z przystawania trojkatow Tak wniosek trojkat jest rownoramienny Prosba bo ja mam chyba jakies zacmienie Wylicz ile wynosi kąt FED na moim rysunku jest tak α+y+[180^o−(α+γ)]=180 ^o Po kolei

6latek: Mozna prosic ? Cos mi nie wychodzi . Eta pewnie boki zrywa . No trudno

Eta:

6latek: Eta dziekuje Ale mozesz zrobic to obliczenie tego kąta ?

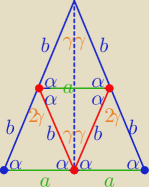
Eta: 2α+2γ=180^o ⇒α+γ=90^o

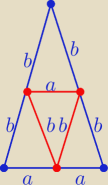
Mila: DBEF− równoległobok− kąty przeciwległe równe albo tak: 2α+γ=180 α+γ+x=180 x=α

6latek: Dziekuje za to rowniez Ale chcialem to z 20 : 58 jesli mozna

Eta: Często zadajesz takie pytania,że "nie wiem o co pytasz"? i po co pytasz?

6latek: α+γ+[180−(α+γ)]=180 α+γ+180−α+γ=180 2γ=0 ⇒γ=0 niemozlie wiec gdzie robie blad zeby obliczyc miare kąta FED ? Te sposoby ktore mi ppokazalyscie to rozumiem

6latek: Chyba ze jest to po prostu ∡FED=∡EFD=180^o−(α+γ) i te kąty sa rowne A obliczenie ktore zastosowalem bylo złe .

Eta: x=|∡FED| α+γ+x=180^o i 2α+γ=180^o to α+γ+x=2α+γ x=α ====

6latek:

Eta: