Oblicz Ok: Dany jest trójkąt ABC o bokach długości |BC| =a, |AC|= b taki, że a ≥b≥|AB| . Wyznacz długość najkrótszego odcinka o końcach należących do boków trójkąta AC i BC, który dzieli trójkąt ABC na trójkąt i czworokąt o równych polach wiedząc, że |∡ACB| = γ Proszę o wskazówki

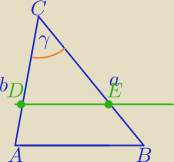
Mila: a ≥b≥|AB| , |∡ACB| = γ 1) DE||AB

	1		1
PΔABC=		a*b*sinγ , PΔCDE=		a*b*sinγ
	2		4

ΔCDE∼ΔABC 2) Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa

PΔCDE		1   a*b*sinγ 4		1
	=		=
PΔABC		1   a*b*sinγ 2		2

	1		1
k2=		⇔k=
	2		√2

	1		√2
|DE|=		*|AB|=		|AB|
	√2		2

|AB|²=a²+b²−2abcosγ ...

Ok: Dziękuję