Przystawanie trojkatow 6latek: https://zapodaj.net/5fd812a268530.jpg.html Bardzo przepraszam ze w takiej to jest formie ale byloby za duzo rysowania Chodzi o zadanie nr 273 i 276 (nr 274 i 275 mam zrobione ) Jesli chodzi o zadanie nr 273 to wedlug mnie a) e) f) to sa trojkaty przystajace

wredulus_pospolitus: a (g) czemu nie masz podobieństwo bkb (wspólny bok mają) więc z tw. cosinusów wiesz że i trzeci bok jest taki sam

wredulus_pospolitus: ΔRTS i ΔRZY jest oczywiste ΔRZU i ΔRSW mają te same dwa kąty (przy Z i S wynika z danych w zadaniu −−− a przy R na podstawie danych zadania) oraz jeden z boków równy (pomiędzy tymi kątami) To oznacza, że |RW| = |RU| więc |YW| = |TU| (bo |RY| = |RT| <−−− wysokości pierwszych dwóch przystających) więc ΔTUP i ΔYWP przystające no i na koniec zostaje nam przystawanie ΔRTP i ΔRYP (wspólny jeden bok, drugi bok równy <wysokości innych trójkątów>, i kąt pomiędzy tymi bokami = przystawanie)

wredulus_pospolitus: Więc i jeszcze zapomniałem o ΔRSP i ΔRZP które są złożeniem dwóch parami przystających trójkątów

Eta: Ja się nie podejmuję ... bo kark można skręcić

wredulus_pospolitus: Jeżeli jeszcze jakieś pary trójkątów pominąłem to z pewnością i one będą przystające ... bo już zbyt wiele rzeczy (kątów i długości boków) jest równa, aby mogło być inaczej

6latek: A b) c) d) dlaczego nie sa ?

wredulus_pospolitus: Jeżeli dobrze policzyłem ... ogólnie powinno być 6 par przystających trójkątów

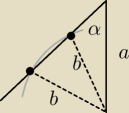
wredulus_pospolitus: (b) dlatego nie (dwa możliwe położenia boku o długości b)

wredulus_pospolitus: (c) ... 'kąt po innej stronie' względem boków a i b

wredulus_pospolitus: (b) 'bok o długości a po innej stronie' względem kątów α i β

6latek: Przepraszam Eta Ja go po zeskanowaniu obrocilem .Nie wiem dlaczego tak sie wstawilo . Artur tam w zadaniu nr 276 to tak zauwazylem ze wszystkie te trojkaty beda przystajace na podstawie cech przystawania trojkatow prostokatnych

Bleee: Przystawania pierwszej pary niesie za sobą przystawanie pozostałych par.

6latek: Bardzo dziekuje za pomoc

Satan: 6latek, taka mała pomoc ode mnie w dziedzinie wrzucania obrazków − w aplikacjach do otwierania zdjęć można znaleźć taką opcję jak "obróć o...". Wystarczy obrócić, zapisać i wrzucić Dzięki temu wszyscy skorzystają

6latek: Czesc Ale do tej pory wstawialem i wszystko bylo dobrze Nie wiem czy od razu tego nie obrocilem po zaimportowaniu ?

Satan: Zdjęcie należy obrócić przed zaimportowaniem pliku, po importowaniu już nie można go obrócić Jeśli używasz Windowsa, to bazowa aplikacja do otwierania zdjęć ma taką funkcję. Spróbuj sobie wgrać nieobrócone zdjęcie, a potem obrócone i zobaczysz, że będzie zaimportowane tak, jak je wrzuciłeś