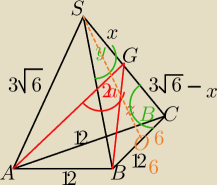
stereometria salv: W ostrosłupie prawidłowym trójkątnym krawędź boczna ma długość 3√6 , a krawędź podstawy ma długość 12. Oblicz miarę kąta utworzonego przez dwie sąsiednie ściany boczne.

	1
Powyliczalem dwa cosinusy w trojkacie BCS.Wyszedl mi cosγ=−		z tw. cos,no i cosβ
	3

	2√6
obliczylem trojkata SOC wyszlo cosβ=		.
	6

Potem znowu tw.cos w trojkatac SGB oraz BGC,czyli

	2√6
z2=(3√6−x)2+144−24(3√6−x)*
	6

z²=x²+54+2√6x odjąłem stronami i wychodzi mi 0=0..Chyba zły pomysł na to zadanie mam

salv: Dodam,że już na internecie sprawdzałem rozwiązania ale chce wiedzieć co tu jest nie tak

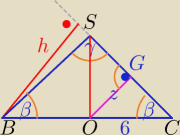
Mila: Otrzymałeś tożsamość:

	1
1) ΔBSC− Δrozwartokątny równoramienny (cos∡S=−		)
	3

2) Przekrój będzie inny niż narysowałeś. 3) Aby znaleźć miarę kąta liniowego między ścianami bocznymi musimy przeciąć płaszczyzną prostopadłą do krawędzi SC. 4) przesuwam h tak, aby spodkiem był środek BC Teraz licz .