geo anal
krumcajs: Geometria Analityczna − analiza wyników
cześć, mam pytanie co do geo. analitycznej
Przeważnie gdy korzysta się z wlasnosci charakterystycznych dla geometrii analitycznej, np.
odleglosc punktu od punktu, punktu od prostej, to powstaje rownanie kwadratowe.
jezeli w zadaniu nie mam jasno podane, ze np. "Wspolrzedne punktu A sa dodatnie/ujemne" to skad
mam wiedziec ktory z x−ów będzie poprawny dla obranego punktu? A moze beda obie rozwiazania
dobre?
przykladowo −
| | 700 | |
"Punkt A = (23,22) jest wierzchołkiem trójkąta prostokątnego o polu |
| . Prosta AC |
| | 3 | |
zawiera przeciwprostokątną tego trójkąta, a prosta zwierająca przyprostokątną AB ma równanie
3y−4x+26=0 . Środek okręgu wpisanego w trójkąt ABC ma współrzędne S = (− 2,− 3) . Oblicz
współrzędne wierzchołków B i C tego trójkąta.
obliczyłem, że x punktu B to może być zarówno −1 jak 5. Skąd mam wiedzieć która z tych
współrzędnych będzie właściwa?
5 kwi 12:08
krumcajs:
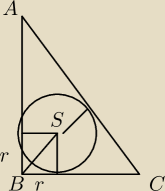
5 kwi 12:10
krumcajs: | | 4x−26 | |
AB zawiera się w prostej pr.AB, zatem B(x, |
| ) |
| | 3 | |
r wyliczam w banalny sposób z odl. prostej od srodka okręgu, r=5
zatem SB=r
√2czyli 5
√2
w ten sposób właśnie wyszlo mi równanie kwadratowe, z ktorego, xB=−1 lub xB=5
jak zweryfikować które będzie wlasciwe?
5 kwi 12:12
ite:
W zadaniach z geometrii analitycznej warto rysunek poglądowy do zadania wykonać w układzie
współrzędnych. Spróbuj tak zrobić, zobaczysz, czemu tylko jedno z tych rozwiązań jest
prawidłowe.
5 kwi 12:56
PW: Analitycznie − trzeba napisać równanie prostej prostopadłej do AB i przechodzącej przez B
(czyli równanie prostej zawierającej bok BC) dla obu wypadków i pokazać, że w jednym z nich
odległość S od tej prostej nie jest równa 5.
5 kwi 13:44
ite:
@PW z moich obliczeń wynika, że w obu przypadkach (oznaczę je B1,B2) odległość prostych
prostopadłych do prostej AB od S jest równa 5.
Na boku AB z rysunku 12:10 są dwa punkty odległe od S o 5√2, ale ten drugi "wyznacza"
(←wybacz mi to określenie) bok trójkąta tak, że zadany okrąg nie będzie wpisany.
5 kwi 13:59
krumcajs:
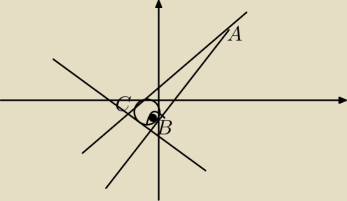
rzeczywiście, jeśli B=5, to By=−2, czyli nad środkiem okręgu, a z wykresu wynika, że B jest
pod.
5 kwi 14:43
krumcajs: Ale co jeśli są zadania, w których jest po prostu za mało danych to narysowania rysunku
podglądowego?
5 kwi 14:43
krumcajs: jeśli Bx=5*
5 kwi 14:44
ite: Na początek trzeba zaznaczyć te punkty, proste, które są podane. W miarę pojawiania się nowych
dorysowywać. Tak jak napisał PW trzeba się oprzeć na obliczeniach; rysowanie jest tylko
sposobem pomocniczym, ale czasem pozwala zobaczyć, gdzie szukać rozwiązań.
5 kwi 14:49
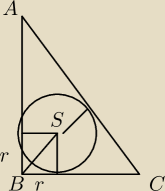
 rzeczywiście, jeśli B=5, to By=−2, czyli nad środkiem okręgu, a z wykresu wynika, że B jest
pod.
rzeczywiście, jeśli B=5, to By=−2, czyli nad środkiem okręgu, a z wykresu wynika, że B jest
pod.