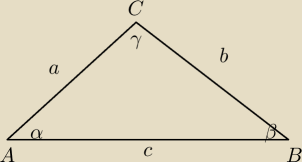
dowód z planimetri LOL ALE PADAKA: Boki trójkąta mają długości a,b,c oraz a²−b²=bc. Wykaż, że α=2β

ABC: można fizycznie z twierdzenia sinusów a pewnie jest też krótszy sposób

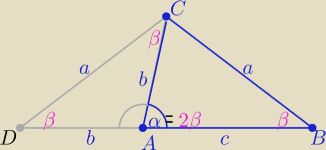
Eta: 1/ przedłużamy odcinek AB do punktu D tak aby ||AC|=|AD|=b wtedy ΔADC jest równoramienny

	a		b+c
2/ z treści zadania a2−b2=bc ⇒		=
	b		a

zatem ΔADC podobny do ΔBDC to ΔBDC i ADC są równoramienne o kątach przy ramionach β czyli |∡α|=2β −−− jako kąt zewnętrzny trójkąta ADC ========= c.n.w.

Feshio: Czy mógłby mi ktoś proszę wytłumaczyć, na jakiej podstawie określamy że |DC|=a ? Bo nie do końca to rozumiem