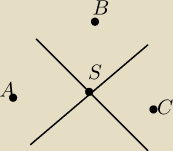
konstrukcja 6latek: Opisz konstrukcje uzasadniajaca twierdzenie : Przez dowolne trzy punkty niewspolliniowe mozna poprowadzic okrag Dlaczego jest tylko jeden taki okrag Jesli poprowadzimy symetralne odcinkow AB i BC to punkt przeciecia sie tych symetralnych bedzie punktem ktory jest rownoodlegly od punktow A B C stad AS=SB=SC Teraz dlaczego istnieje jeden taki okrag ?

ite: Dwa różne punkty mają tylko jedną symetralną, więc każda para (utworzona z tych punktów) ma jedna symetralną. Pokaż, że te trzy symetralne mają tylko jeden pkt wspólny. Jeden pkt będący środkiem+ustalony promień→ jeden okrąg.

jc: Zbiór punktów S takich, że AS=BS jest prostą. Zbiór punktów S takich, że AS=CS jest prostą. Proste te nie są równoległe bo wtedy punkty A, B, C byłyby współliniowe. Mają więc jeden punkt wspólny S. Wtedy AS=BS=CS, i jest jedyny punkt o tej własności. Okrąg o środku S i promieniu AS jest jedynym okręgiem zawierającym A, B, C (każdy inny okrąg miałby ten sam środek i ten sam promień, a więc byłby tym samym okręgiem).

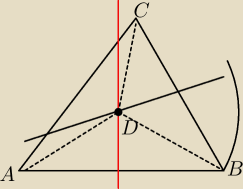
6latek: W trojkacie ABC punkt D jest punktem przeciecia sie symetralnej boku AB i BC Poniewaz D lezy na symetralnej boku AB wiec mamy AD=BD Rowniez punkt D lezy na symetralenj boku BC stad BD=CD Z tych rownosci wynka rowniez nastepna rownosc a mianowicie AD=CD wobec tego punkt D lezy rowniez na symetralnej boku AC czyli punkt D jest rowno oddalony od kazdego z punktow A B C tzn AD=BD=CD Wynika z tego ze punkty A B C leza na jednym okregu o srodku D

6latek: Dzien dobry jc

6latek: jc Czytajac i przepisujac do zeszytu Twoje wytlumaczenie doszedlem do wniosku ze jest jedno z nalepszych wytlumaczen Masz moze podobne do wspolnego punktu dla dwusiecznych i wysokosci ?