. arti: w polkole o promieniu r wpisano prostokat o najwiekszym polu. oblicz cosinus kata rozwartego miedzy przekatnymi tego prostokata

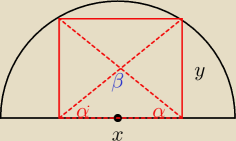
wredulus_pospolitus: 1) znajdź boki (x,y) tego trójkąta (o największym polu)

	x
2) cos β = cos(180 − 2α) = −cos(2α) = −( 2cos2α − 1) = 1 − 2cos2α = 1 − 2*
	√x2+y2

arti: jak znalezc x i y ? probowalem juz z pitagorasa i z tw. cosinusow ale za duzo niewiadomych

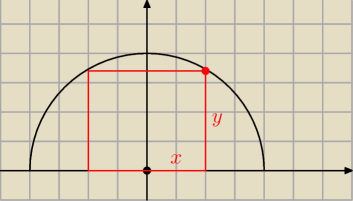wredulus_pospolitus: f(x) = √r² − x² P(x) = 2x*√r²−x² <−−−− szukasz maksimum prostokąt ma boki: 2x, √r²−x² po wyliczeniu ich podstawiasz do wcześniej podanej postaci

wredulus_pospolitus: analogicznie robisz to zadanie ze stożkami

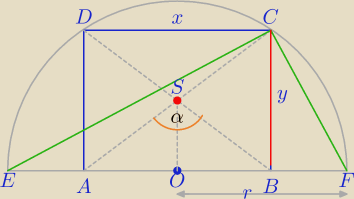Mila: P_▭=x*y 1) ΔECF− Δprostokatny, |∡C|=90 jako kąta wpisanego w okrąg opartego na średnicy⇔ y²=|EB|*|BF|

	x
|BF|=r−		,
	2

	x		x		x
y2=(r+		)*((r−		) i r−		>0⇔0<x<2r
	2		2		2

	x2
y2=r2−
	4

y=√r²−^x2₄ 2) P(x)=x*√r²−^x2₄

	−0.5x
P'(x)=1*√r2−x24+x*		=
	2√r2−x24

	x2   2*(r2− )−0.5x2   4
=
	2√r2−x24

P'(x)=0⇔2r²−x²=0 x²=2r², x=r√2, y=√r²−2r²/4=√r²/2

	r
x=r√2, y=
	√2

3)

	x		y		5
W ΔSOB: |SB|2=(		)2+(		)2⇔ |SB|2=		r2
	2		2		8

W ΔASB:

	5		5		5
(r√2)2=		r2+		r2−2*		r2*cosα
	8		8		8

	5		5
2r2−		r2=−		r2*cosα
	4		4

3		5
	=−		cosα
4		4

	3
cosα=−
	5

============

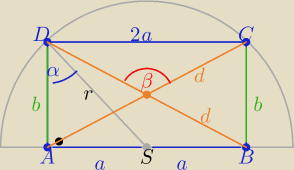Eta: Zadanie można rozwiązać ( bez pochodnych ) tak: w ΔADS : b=r*cosα i a=r*sinα to P(ABCD)=2r²sinα*cosα ⇒ P=r²*sin(2α) −−− jest największe gdy sin(2α)=1 zatem α= 45^o i P=r²

	5
to b=r√2/2 i 2a=r√2 więc d2=(2a)2+b2 ⇒ d2=		r2
	2

	1		1		5		4
P(ABCD)=		d2*sinβ to		*		r2sinβ=r2 ⇒ sinβ=
	2		2		2		5

więc cosβ= −√1−sin²β ( dla kąta rozwartego)

	3
cosβ= −
	5

============== i po ptokach

Eta: Jak widać arti ma to w...............

wredulus_pospolitus: zobaczył gotowca, przepisał i 'zniknął'

Mila: arti, taki już jest. Zerknie tu za dwa dni i o coś zapyta