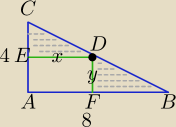
Zadanie optymalizacyjne Lkl: Na przeciwprostokątnej BC trójkąta prostokątnego o przyprostokątnych 4 i 8 wybieramy punkt D i wpisujemy prostokąt. Oznaczmy przez x odległość punktu D od a) krótszej b) dłuższej przyprostokątnej. Wyznacz wzór funkcji P opisującej pole które pozostanie w trójkącie ABC po usunięciu prostokąta. Wyznacz dziedzinę tej funkcji. Dla jakiej wartości x pole będzie najmniejsze?

Mila: P_Δ=16 P_f=16−x*y EDEC∼ΔBAC⇔

EC		4		4−y		1
	=		⇔		=		⇔x=8−2y
x		8		x		2

	1		1
y=−		x+4 0<−		x+4<8⇔x∊(0,8)
	2		2

	1
Pf(x)=16−x*(−		x+4)
	2

	1
P(x)=		x2−4x+16
	2

	4
Pmin dla x=		=4
	2*0.5

P(4)=8