pomocy kropka: 1.Wyznacz równanie symetralnej odcinka o końcach A=(−7,2) i B=(5,−6) 2.Wyznacz x z równania 1+5+9+13+...+x=780

ABC: 1) znajdź środek odcinka AB i poprowadź przez ten środek prostą prostopadłą do prostej zawierającej odcinek AB

zys: 2. a₁=1 r=4

	1+(n−1)*4
780=		*n
	2

Policzysz n a potem a_n czyli x

kropka: zys: wyszło mi 4n⁻3n−1560 i nie wiem gdzie zrobiłam błąd

kropka: ABC: środek to −1, −2 ?

6latek: Srodek to S=(−1,−2)

kropka: no to dobrze mam i wtedy trzeba jeszcze jakiś wzór wyznaczyć?

6latek: Co wiesz o symetralnej odcinka ?

lisek: no, że to musi byc prosta prostopadła do odcinka AB i przechodzić przez jego środek no i mam ten środek wyliczony

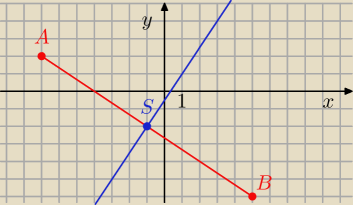
janek191: z.1 A = (− 7, 2) B = ( 5, −6) więc środek odcinka AB

	− 7 + 5		2 −6
S = (		,		) = ( −1, −2)
	2		2

Współczynnik kierunkowy prostej AB :

	− 6 − 2		−8		2
a =		=		= −
	5 − (−7)		12		3

więc współczynnik prostej prostopadłej do pr AB :

	3
a1 =
	2

Prosta prostopadła do pr AB ( dowolna):

	3
y =		x + b
	2

Ma być symetralną, więc musi przechodzić przez S = ( − 1, −2), dlatego

	3
− 2 =		*(−1) + b
	2

	3
− 2 =−		+ b
	2

	1
b = −
	2

	3
Odp. y =		x − 0,5
	2

y = 1,5 x − 0,5 ==============

janek191: z.2 1 + 5 + 9 + ... + x = 780 Mamy a₁ = 1 r = 4 więc a_n = a₁ + ( n −1)*r = 1 + ( n −1)*4 = 4 n − 3

	a1 = an		1 + 4 n − 3
Sn =		*n =		*n = (2 n −1)*n = 2 n2 − n = 780
	2		2

2 n² − n − 780 = 0 Δ = 1 − 4*2*(−780) = 1 + = 6241 √Δ = 79

	1 + 79
n =		= 20
	4

x = a₂₀ = 4*20 − 3 = 77 ===================

Eta: zad1/ S(−1,−2)

	2
aAB=−
	3

	1
sym. s: y=−		(x−xS)+yS
	aAB

	3
s: y=		(x+1)−2
	2

y=1,5x−0,5 ================

PW: Zadanie z symetralną można też rozwiazac korzystając z faktu, że punkty symetralnej są jednakowo oddalone od końców odcinka. Punkt P=(x, y) leżący na symetralnej spełnia więc równanie |PA| = |PB| − spróbuj tak zrobić.

jc: Nic nowego, ale inaczej zapisane. Symetralna odcinka o końcach A=(−7,2) i B=(5,−6)

	1
przechodzi przez środek odcinka, czyli przez punkt S=		(A+B) = (−1, −2)
	2

i jest prostopadła do wektora B−A=(12,−8) || (3,−2), a więc opisana jest wzorem: 3x−2y=3*(−1)−2*(−2)=1.

Eta:

PW: Sposób z 12:59 (6 kwietnia) jest o tyle dobry, że nie trzeba wiedzieć nic oprócz wzoru na odległość dwóch punktów. |PA|² = (x+7}² + (y−2)² = x²+14x+49+y²−4y+4 = x²+14x+y²−4y+53 |PB|² = (x−5)²+(y+6)² = x²−10x+25+y²+12y+36 = x²−10x+y²+12y+61 Przyrównanie prawych stron daje 14x−4y+53 = −10x+12y +61 24x−16y−8 = 0 3x−2y−1 = 0 − równanie symetralnej.