zadanie dotyczące ciągów liczbowych, poziom technikum Weronika: Mam problem z zadaniami, ktoś może pomóc? 1. Wyrazami ciągu arytmetycznego są kolejne liczby naturalne, które przy dzieleniu przez 7 dają resztę 4. Wyraz pierwszy jest mniejszy od 12. Oblicz a₆₃ 2. Wyznacz wszystkie liczby czterocyfrowe, w których cyfra setek jest o 2 większa od cyfry jedności i trzy razy większa od cyfry setek. 3. Promień okręgu opisanego na trójkącie prostokątnym ma długość 30 cm, a długość promienia okręgu wpisanego w niego wynosi 1 dm. Oblicz obwód i pole tego trójkąta.

Weronika: zrobiłam 3 z 6 zadań, może wskazówki jak to wyżej rozwiązać? Ktokolwiek?

6latek: W zadaniu nr 1 sprobuj a₁=11 bo 11: 7= 1 i r 4 i 11<12 Jesli co bedzie nie halo to wez a₁= 4 bo 4: 7= 0 i r 4

ABC: w pierwszym zadaniu są dwie liczby naturalne mniejsze od 12 które dają resztę 4 przy dzieleniu przez 7, są to 4 i 11 czyli 1) a₁=4 a₆₃=a₁+62r=4+62*7=4+434=438 albo 2)a₁=11 a₆₃=a₁+62r=11+62*7=11+434=445

ABC: w drugim zadaniu jeżeli dobrze przepisałaś "cyfra setek trzy razy większa od cyfry setek" to cyfrą setek musi być zero

Weronika: Przepraszam, w czwartym zamiast trzy razy większa od cyfry setek ma być dziesiątek.

Weronika: Dziękuje wam za pomoc. Pierwsze zadanie przynajmniej rozumiem.

Weronika: Utknęłam z tym 3. Ktokolwiek?

ABC: Weronika co możesz powiedzieć o długości przeciwprostokątnej tego trójkąta?

6latek: jesli R=30 cm to c=2R=60cm r=10cm znasz jakas zaleznosc miedzy promiem wpisanym w trojkat prostokatnt a bokami ? spojrz w tablice maturalne Prosze zrobic rysunek

Eta: R=30 =3 dm , r=1dm P=r(r+2R)=........... L= 2r+2R=.......... i po ptokach

Eta: Poprawiam chochlika L=2R+4R

ABC:

Eta: Jest dobrze, dobrze

Eta: No tak z małą poprawką (chochlika co namieszał) L=2r+4R

ABC: are you sure? L=6R ?

Eta: ................. czytaj ostatni wpis

ABC: bez rysunku Weronika i tak tego nie obczai a wiesz jak ja rysuję

ABC: chociaż szkic rozwiązania mogę napisać − jako pierwszy obliczamy obwód korzystając z tego że przeciwprostokątna 2R i równości odcinków stycznych − jako drugie obliczamy pole ze wzoru S=rp gdzie p−połowa obwodu

Eta:

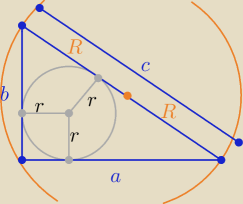
	1		a+b−c
R=		c i r=		−−−− wzory z tablic
	2		2

to c=2R i 2r=a+b−c ⇒ a+b=2r+2R L=a+b+c = 2r+2R+2R ⇒ L=2r+4R a²+b²=c² ⇒ (a+b)²−2ab=c² to (2r+2R)²−(2R)²=2ab (2r+2R+2R)(2r+2R−2R)=2ab 2(r+2R)*2r=2ab /:4

	ab
r(r+2R)=		=P
	2

P=r(r+2R)

Eta: lub P=r*p 2p=L=2r+4R = 2(r+2R) to p=r+2R P=r(r+2R)

ABC: no, tak szybciej jest

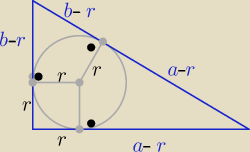
Eta: Można jeszcze tak P=(b−r)(a−r) P=ab−r(a+b)+r²

ab
	=ab−r(2r+2R)
2

	ab
r(r+2R)=		=P
	2

Eta: A Weronika i tak ma to w....................

weronika : dziękuje

6latek: Moze jest grzeczna dziewczynka i poszla spac

weronika : nie śpię, z pracy dopiero wyszłam 😂