Największe pole PirchHD: Dana jest parabola y=8−x². Wyznacz największą wartość pola prostokątna ABCD zawartego pomiędzy osią ox a parabola którego wierzchołki A i B leżą na osi OX, a wierzchołki C i D położone na paraboli. Może ktoś to narysować? Lub dać jakąś poradę

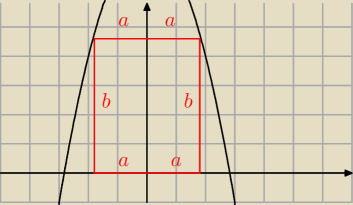
wredulus_pospolitus: masz prostokąt o bokach: 2a, b zauważ, że f(a) = b ... więc Twój prostokąt ma boki: 2x ; 8−x² P(x) = 2x*(8−x²) szukasz maksimum

PirchHD: Ja zrobiłem tak że odcinek od punktu A(x,0) i B(−x,0) Obliczylem długość tego odcinka czyli |AB|=pierw x². Tak samo AD= pierwiastek(x−8)². Wtedy p(x)= AB *AD. Czy moke rozumowanie jest dobre ? Oczywiście wtedy mamy bezwzględną wartość

wredulus_pospolitus: jest błędne |AB| = √(x−(−x))² + (0 − 0)² = √(2x)² = |2x|