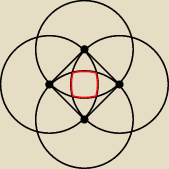
 Dany jest kwadrat o boku długości 3, z każdego jego wierzchołka zakreslono koło o promieniu
równym 3. Oblicz pole częsci wspólnej tych kół.
Dany jest kwadrat o boku długości 3, z każdego jego wierzchołka zakreslono koło o promieniu
równym 3. Oblicz pole częsci wspólnej tych kół.
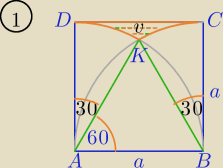 1) Pole trójkąta krzywoliniowego DCK:
1) Pole trójkąta krzywoliniowego DCK:
| 1 | a2√3 | |||
PDCK=32− | π*a2− | |||
| 6 | 4 |
| 1 | 9√3 | |||
PDCK=9− | π*32− | |||
| 6 | 4 |
| 3π | 9√3 | |||
PDCK=9− | − | |||
| 2 | 4 |
| 3π | 9√3 | |||
v=9− | − | |||
| 2 | 4 |
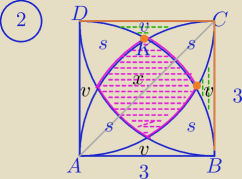 cd
cd
| 3π | 9√3 | |||
v=9− | − | |||
| 2 | 4 |
| 1 | 9 | |||
s+2v=9− | *π*32=9− | π | ||
| 4 | 4 |
| 3 | 9√3 | 9 | ||||
s+2*(9− | π− | )=9− | π | |||
| 2 | 4 | 4 |
| 3 | 9√3 | |||
s= | π−9+ | |||
| 4 | 2 |
| 3 | 9√3 | 3 | 9√3 | |||||
9=4*( | π−9+ | )+4*(9− | π− | )+x | ||||
| 4 | 2 | 2 | 4 |