Kiełbasa, próba matura III-PR, Zadanie 11.
PGinf: Kąty BAD i ABC czworokąta ABCD mają miary równe 60°.
Długość boku AB jest równa sumie długości boków AD i BC.
Wykaż, że środek boku CD jest jednakowo odległy od środków boków AD i BC.
3 kwi 07:40
PGinf: Jest ktoś zdolny, jak ktoś potrafi to bardzo bym prosił
4 kwi 00:03
iteRacj@:
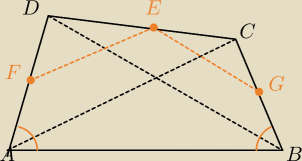
|<BAD| =|<ABC|=60
o, |DE|=|EC|
z tw.cosinusów w ΔABC |AC|
2=|AB|
2+|CB|
2−2|AB||CB|cos 60
o
z tw.cosinusów w ΔADB |DB|
2=|AB|
2+|AD|
2−2|AB||AD|cos 60
o
|AB|=|AD|+|BC| ⇒ |AB|
2=|AD|
2+|BC|
2+2|AD||BC|
cos 60
o=1/2
|AC|
2=|AB|
2+|CB|
2−(|AD|+|BC|)|CB|=|AB|
2−|AD||CB|
|DB|
2=|AB|
2+|AD|
2−(|AD|+|BC|)|AD|=|AB|
2−|AD||CB|
⇒ |AC|
2=|DB|
2 przekątne czworokąta są równe
w ΔADB |FE|=1/2|AC| // FE odcinek łaczący środki boków trójkąta
w ΔDBC |EG|=1/2|DB| // EG odcinek łaczący środki boków trójkąta
⇒ |FE|=|EG|
4 kwi 00:49
 |<BAD| =|<ABC|=60o, |DE|=|EC|
z tw.cosinusów w ΔABC |AC|2=|AB|2+|CB|2−2|AB||CB|cos 60o
z tw.cosinusów w ΔADB |DB|2=|AB|2+|AD|2−2|AB||AD|cos 60o
|AB|=|AD|+|BC| ⇒ |AB|2=|AD|2+|BC|2+2|AD||BC|
cos 60o=1/2
|AC|2=|AB|2+|CB|2−(|AD|+|BC|)|CB|=|AB|2−|AD||CB|
|DB|2=|AB|2+|AD|2−(|AD|+|BC|)|AD|=|AB|2−|AD||CB|
⇒ |AC|2=|DB|2 przekątne czworokąta są równe
w ΔADB |FE|=1/2|AC| // FE odcinek łaczący środki boków trójkąta
w ΔDBC |EG|=1/2|DB| // EG odcinek łaczący środki boków trójkąta
⇒ |FE|=|EG|
|<BAD| =|<ABC|=60o, |DE|=|EC|
z tw.cosinusów w ΔABC |AC|2=|AB|2+|CB|2−2|AB||CB|cos 60o
z tw.cosinusów w ΔADB |DB|2=|AB|2+|AD|2−2|AB||AD|cos 60o
|AB|=|AD|+|BC| ⇒ |AB|2=|AD|2+|BC|2+2|AD||BC|
cos 60o=1/2
|AC|2=|AB|2+|CB|2−(|AD|+|BC|)|CB|=|AB|2−|AD||CB|
|DB|2=|AB|2+|AD|2−(|AD|+|BC|)|AD|=|AB|2−|AD||CB|
⇒ |AC|2=|DB|2 przekątne czworokąta są równe
w ΔADB |FE|=1/2|AC| // FE odcinek łaczący środki boków trójkąta
w ΔDBC |EG|=1/2|DB| // EG odcinek łaczący środki boków trójkąta
⇒ |FE|=|EG|