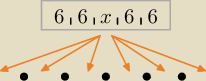
Prawdopodobieństwo genewra: Rzucamy dziesięć razy sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w tych dziesięciu rzutach otrzymaliśmy dokładnie cztery razy sześć oczek, przy czym wyrzucono je w następującej konfiguracji ...66x66... tzn. w pewnym momencie w dwóch kolejnych rzutach otrzymaliśmy szóstki, potem wyrzuciliśmy inną liczbę x oczek, a następnie znowu wyrzuciliśmy dwie szóstki w dwóch kolejnych rzutach.

a7:

	3*2*56		56
czy wynik jest		=
	610		69

wredulus_pospolitus:

10 4   *56
610

genewra: Ile wynosi Ω? 6¹⁰? Te 6¹⁰ trzeba potęgować, czy może zostać w takiej postaci?

PW: Podciąg (6, 6, x, 6, 6) przy konkretnym wybranym x∊{1, 2, 3, 4, 5} może w 10−elementowym ciągu zająć 5 pozycji. Wobec tego prawdopodobieństwo zdarzenia A opisanego w zadaniu jest równe

	5•56
P(A) =
	610

PW: Za wcześnie kliknąłem. Licznik wziął się z tego, że 5 pozycji, a pozostałe 6 elementów ciągu (łącznie z tym między szóstkami) może stanowić dowolna liczba spośród pięciu. Odp.

	57
P(A) =		.
	610

Jest to już trzecia odpowiedź, i każda inna. Kto da więcej? Odpowiedź na pytanie z 00:30: − Można tak zostawić, w tych zadaniach idzie o metodę liczenia, a nie o wynik w postaci ułamka (chyba że wyraźnie mówią coś o wyniku, np. "Podaj wynik z dokładnością do trzech miejsc po przecinku").

ite: @PW Czy podciąg (6, 6, x, 6, 6) nie może w 10−elementowym ciągu zająć 6 pozycji?

PW: Patrzmy na ostatnią szóstkę. Może ona być: 1. piątym wyrazem ciągu, 2. szóstym wyrazem ciągu, 3. siódmym wyrazem ciagu, 4. ósmym wyrazem ciągu, 5. dziewiątym wyrazem ciągu, 6. dziesiątym wyrazem ciągu. No i masz rację, Liczyłem na palcach, ale się pomyliłem, musze odszczekać W takim razie odpowiedź brzmi

	6•56
P(A) =
	610

− a7 miała rację.

iteRacj@: Dziekuję, już wszystko jasne.