funkcja kwadratowa Nerwicaodnauki: W prostokątnym układzie współrzędnych wyznacz zbiór tych wszystkich punktów o współrzędnych ( m, n) takich, że funkcja o wzorze f(x) = x2−2mx−n+1 ma dwa różne miejsca zerowe należące do przedziału (−1,1). zadanie jest juz na forum, jednak zostaje przy 2 niewiadomych i nie wiem co dalej... a czy warunek xw ∊ (−1.1) jest konieczny? nigdy w szkole sie z takim nie spotkalem

wredulus_pospolitus: Warunki: 0) Δ > 0 (aby były dwa miejsca zerowe) 1) f(−1) > 0 ( to oznacza, że oba miejsca zerowe będą 'na lewo' albo 'na prawo' do x = −1) 2) f(1) > 0 ( to oznacza, że oba miejsca zerowe będą 'na lewo' albo 'na prawo' do x = 1) 3) x_w ∊ (−1;1) ( a to nam gwarantuje <w połączeniu z poprzednimi>, że oba miejsca będą w przedziale (−1;1) )

wredulus_pospolitus: Nie patrzyłem na tamto rozwiązanie, więc nie wiem czy zrobili takie same warunki

wredulus_pospolitus: mam nadzieję, że teraz rozumiesz dlaczego warunek co do x_w jest istotny

Nerwicaodnauki: dobra no to wiedzialem wlasnie , ale zostaje z dwoma neiwiadomymi i nie wiem co dalej

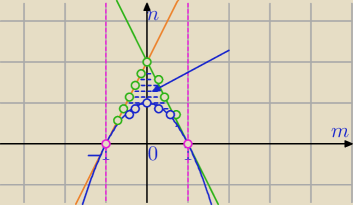
Mila: f(x) = x²−2mx−n+1 1) Δ>0⋀ x₁,x₂,x_w∊(−1,1) Δ=4m²−4*(−n+1)⇔ (*) m²+n−1>0⇔n>−m²+1 wykres f(m)=−m²+1 punkty nad parabolą 2) i

	2m
xw=		=m
	2

−1<m<1 i f(−1) >0 i f(1)>0⇔1+2m−n+1>0 i 1−2m−n+1>0 ⇔n<2m+2 i n<−2m+2 punkty poniżej tych prostych , nad parabolą i tylko dla m∊(−1,1)

Mila: