rozwiąż nierówność
Kinga8: |x+2|− |x|> 0,
czyli wyznaczam miejsca zerowe :−2, 0
1)w przedziale (−∞;−2) :
−(x+2)−(x)> 0
−x−2−x > 0
czyli x<−1
2)w przedziale [−2;0)
x+2−x> 0
3) w przedziale [0;+∞)
x+2+x> 0
czy to jest poprawne rozumowanie, mam problem ze znakami...
2 kwi 19:26
6latek: Rozumowanie poprawne nie jest
1 przedzial
−(x+2)−(−x)>0
2 przedzial
x+2−(−x)>0
3 przedzial
x+2−x>0
2 kwi 19:34
PW: 1) w przedziale (−∞, −2) badana nierówność jest równoważna nierówności x<−1. Wniosek (jaki jest
zbiór rozwiazań w tym przedziale)?
2 kwi 19:35
Eta:
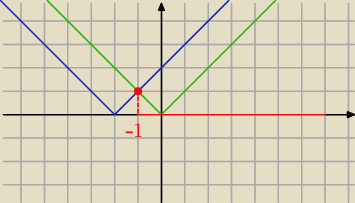 |x+2|
|x+2|>
|x|
x∊(−1,
∞)
========
2 kwi 19:35
PW: A rzeczywiście nierówność jest ułożona źle, więc moja uwaga nieaktualna.
2 kwi 19:38
ICSP: |x + 2| > |x|
(x + 2 + x)(x + 2 − x) > 0
x + 1 > 0
x > −1
2 kwi 20:45
PW: Uczyć się od
ICSP 
Jaki piękny sposób w trzech linijkach, bez tego 'rozbijania na
przedziały".
2 kwi 21:08
Mila:
Bez przedziałów:
|x+2|> |x| /2
x2+4x+4>x2
4x>−4
x>−1
2 kwi 21:11
Kinga8: Rzeczywiście pięknie tylko skąd to się bierze, ICSP

Mila

2 kwi 23:23
ABC:
jeżeli obie strony nierówności są nieujemne to możesz podnieść stronami do kwadratu i nie
zmieniasz zbioru rozwiązań

2 kwi 23:27
 |x+2|>|x|
x∊(−1,∞)
========
|x+2|>|x|
x∊(−1,∞)
========
 Jaki piękny sposób w trzech linijkach, bez tego 'rozbijania na
przedziały".
Jaki piękny sposób w trzech linijkach, bez tego 'rozbijania na
przedziały".
 Mila
Mila
