geometria Nerwicaodnauki: Dany jest równoległobok ABCD, w którym boki mają długość 2cm i 6cm, a pole wynosi 8cm2. Oznaczmy środki boków AB i BC odpowiednio jako punkty P i Q. a) Oblicz długości przekątnych równoległoboku ABCD b) Oblicz pole czworokąta APQD

wredulus_pospolitus: 2) zauważ, że:

	boku * pół wysokości + pół boku * pół wysokości
szukane pole = pole równoległoboku −
	2

wredulus_pospolitus:

	1
pole tego górnego trójkąta wynosić będzie		pola równoległoboku,
	4

	1
a pole dolnego będzie dwa razy mniejsze czy będzie równe		pola równoległoboku
	8

Nerwicaodnauki: czyli pole mam dobrze, a przekatne?

wredulus_pospolitus: to pokaż jak przekątne liczysz ... szczerze ... mi się nie chce tego liczyć (leniwy po weekendzie jestem )

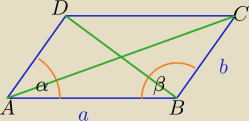
Mila: a) a=6,b=2 P_ABCD=8 1) P_ABCD=a*b*sinα⇔

	8		2
8=2*6*sinα⇔sinα=		=
	12		3

α− kat ostry

	√5		√5
cosα=√1−49=		, cos β=−
	3		3

2) W ΔBAD: |DB|²=6²+2²−2*2*6 cosα |DB|²=40−8√5 |DB|=√40−8√5 |AC|²=|DB|²=6²+2²+2*2*6 cosα |AC|=√40+8√5 ==================

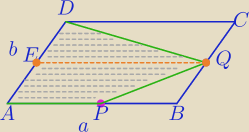
Mila: b)P_ABCD=8

	1
PEQCD=		PABCD=2
	4

	1		1
PAPQE=		*PABCD−		*PABCD=4−1=3
	2		8

P_APQE=2+3=5 ============