geometria Nerwicaodnauki: W rombie cosinus kąta ostrego jest 4/5 a suma długości boku i wysokości jest rówan 8√5 oblicz długość przekątnych tak wiem ze to zadnaie juz bylo, jednak nie jest rozwiazane i nie wiem jakie wyniki powinny byc ostatecznie, prosze o pomoc

wredulus_pospolitus: a chociaż rysunek zrobiłeś/−aś?

wredulus_pospolitus:

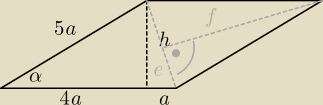
	4		3
cos α =		−> sinα =		−> h = 3a
	5		5

więc: 5a + h = 5a + 3a = 8√3 −> a = √3 więc masz bok 5a = 5√3 i wysokość h = 3√3

	(2e)*(2f)
P = (5a)*h = 45 = 2ef =		= P
	2

więc: 2ef = 45 e² + f² = (5a)² = 75 rozwiązujesz ten układ równań

Nerwicaodnauki: to wiem tylko jakie wyniki są, przekatne mi wyszly 5√2 i 15√2 a pole 50, i chce wiedziec czy to dobre wyniki,tylko to

wredulus_pospolitus: Mi wyszło inne pole ... szukaj błędu u siebie bądź u mnie

wredulus_pospolitus: dobra ... błąd jest u mnie bo 5a+h = 8√5 Ale to nadal P = (5a)*h = 75

ABC: wredulus skąd tam się wziął √3 ?

Nerwicaodnauki: tak pole to 75, mam to na kartce, nei wiem dlaczego napisalem 50, ale te przekatne i to 75 jest dobrze? a tam co ABC pytasz to chyba chodzilo o peirwiastek z 5 tylko blad przy pisaniu sie pojawil

wredulus_pospolitus: tak ... dobre przekątne Ci wyszły

ABC: dobrze Ci wyszło, można pododawać i poodejmować stronami, układ (e+f)²=200 (e−f)²=50 i ponieważ e,f >0 to z tego e+f=10√2, e−f=5√2 , czyli e=7.5 √2, f=2.5 √2

Nerwicaodnauki: u ciebie to e i f to polowy przekatnych?

ABC: tak jak wredulus to oznaczył

ABC: chociaż właściwie przy jego rysunku to f−e=5√2 i f jest ta dłuższa

Nerwicaodnauki: ale u niego to e nei wiadomo cyz wlasnie to cala czy polowka

ABC: ja założyłem że u niego e,f to połowy przekątnych, bo wypisał wzór na pole

	2e 2f
S=
	2

Mila: p=5√2, q=15√2− dł. przekątnych P=75− pole rombu