zadanie na dowodzenie emi: Odcinek CD jest wysokością trójkąta równoramiennego ABC , w którym |AC | = |BC | . Punkt L jest rzutem punktu K wysokości CD na bok AC . Udowodnij, że trójkąt CLD jest podobny do trójkąta CKB .

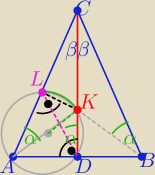
Eta: 1/rys. zgodny z treścią zadania 2/na czworokącie ADKL da się opisać okrąg o średnicy AK ( dlaczego? 3/ kąty wpisane LAK i LDK mają równe miary α ( dlaczego? 4/ wysokość CD jest symetralną trójkąta to i |∡CBK|= α i |∡LCD|=|∡KCB|=β 5/ z cechy (kkk) ΔCLD ∼ΔCBB c.n.w.

emi: okej Na ΔADKL mozna opisać okrąg więc kąty CAK i CDL są równe, a miara kąta CAK=miara kąta CBK. Skoro wysokość CD jest dwusieczną kąta ACB to oznacza, ze nasze trójkąty mają juz dwa kąty o takiej samej mierze. Więc ΔCLD podobny do ΔCKB

emi: dzięki