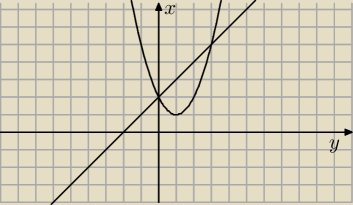
całka Oliwia: Oblicz pola obszarow ograniczonych krzywymi y=x−2 x=2−2y+y² czy tak mniej wiecej bedzie wygladal wykres? i pozniej trzeba przyrownac y+2=2−2y+y² 3y−y² wiec granica calkowanie po y bedzie od 0 do 3 a x mamy funkcje u gory 2−2y+y² a na dole x−2 i jak dalej ulozyc całke?

ABC: Oliwia, x=2−2y+y² to jest parabola, tylko inaczej położona niż zwykle

piotr:

	9
∫03 (y+2−(2−2y+y2))dy =
	2

ABC: sorry Winnetou ale to nie taka parabola

piotr: a niby jaka?

piotr: obróć sobie monitor

ABC: osie zamieniłeś ty cwaniaku, ale przy tym zmieniłeś orientację układu współrzędnych

jc: Jeden rysunek, więc trudno mówić o zmianie orientacji (pomijając fakt, że i tak wykresy rysujemy z dokładnością do podobieństwa).

ABC: klasyczny szkolny układ jest tak zorientowany że aby najkrótszą drogą nałożyć oś x na oś y idziemy przeciwnie do wskazówek zegara − to miałem na myśli

Koko: Tylko to miało być zrobione z całki podwójnej

ABC: no to scałkuj po odpowiednim obszarze funkcję stałą równą 1 − jaki problem?

Koko: Tak Juzbwiem jak to zrobić tylko mam problem w zapisie a prowadzący czepia się o zapis

Koko: 0. y+2 ∫dx ∫dy 3. 2−2y+y² i potem jak ?

ABC: mnie dawno temu uczyli tak y zmienia się od 0 do 3 dla ustalonego y, x zmienia się od 2−2y+y² do y+2 czyli masz całkowanie: ∫₀³( ∫ dx) dy w tej wewnętrznej nie pisałem granic bo za długie ale od 2−2y+y² do y+2