czworokat
6latek:
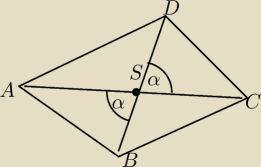
Udowodnij ze jesli przekatne czworokata przecinaja sie we wspolnym srodku to czworokat ten
jest rownoleglobokiem
Z przystawania trojkatow ASB i DSC cecha BKB wynika rownosc bokow ABi CD
Z przystawania trojkatow ASD i BSC cecha BKB wynika rownosc bokow BCi AD
Mam na razie to ze przeciwlegle boki sa rowne
czy trzeba wykazac ze przeciwlegle kąty sa rowne ?
31 mar 23:05
iteRacj@:
Z twierdzenia odwrotnego do twierdzenia Talesa wynika równoległość prostych AB i DC.
31 mar 23:08
6latek: jak mam tutaj zastosowac to tweirdzenie bo Tales na razie nie jest mi bliski .
31 mar 23:11
wredulus_pospolitus:
6−latek ... naprawdę ... tw. Talesa nie tykałeś a trzaskasz geometrię? tw. Talesa to pierwsze
klasy podstawówki są
31 mar 23:12
wredulus_pospolitus:
możesz skorzystać z tw. cosinusów (jeżeli je przerabiałeś
)
31 mar 23:13
iteRacj@: Mnie też bliski nie jest!
Jaką masz podaną definicję równoległoboku?
31 mar 23:13
iteRacj@: O wredulusowi Tales jest bliski, to dobrze : )
31 mar 23:14
6latek: Wiem Artur
7 klasa podrecznik Bialas Straszewicz
Nadrobie tylko nie krzycz na mnie
31 mar 23:19
6latek: Rownoleglobokiem nazywamy czworokat majacy dwie pary bokow rownoleglych
31 mar 23:21
iteRacj@: To wykaż równoległość boków z Talesa albo z równości kątów.
31 mar 23:24
wredulus_pospolitus:
iteracja − mi każdy matematyk jest bliski (sercu)
31 mar 23:27
6latek: Z Talesa to nie wiem bo nawet nie widze kąta przcietego dwoma prostymi rownoleglymi Z rownosci
kątow tez nie wiem bo to ze mam boki rowne to wcale nie oznacza ze sa one rownolegle
31 mar 23:32
iteRacj@: To dobrze
31 mar 23:33
iteRacj@: Ta równość kątów wynika z przystawania trójkątów.
31 mar 23:34
6latek: Tak nawiasem mowiac dla mnie przydalaby sie teraz matematyczka
Tylko gdzie jej szukac
31 mar 23:34
6latek: No tak .Jasne
31 mar 23:36
iteRacj@:
Polskie Towarzystwo Kobiet w Matematyce
31 mar 23:38
6latek: 
31 mar 23:42