matura Guest : 1)Dla jakich wartości parametru p równanie llx−1l−2l=2p−3 ma dokładnie dwa rozwiązania ? p=1,5 ? Tak chyba powinno być, ale wydaje się to za łatwe nie wiem czy nie ma tu haczyka 2) Suma odwrotności pewnych trzech różnych liczb naturalnych jest liczbą całkowitą. Jakie to liczby ? Sprowadziłem do wspólnego mianownika i nie wiem co dalej 3) Uzasadnij, że do wykresu funkcji f(x)=3/5*x+5/3 nie należy żaden punkt o obu współrzędnych całkowitych (tzw. punkt kratowy).

wredulus_pospolitus: 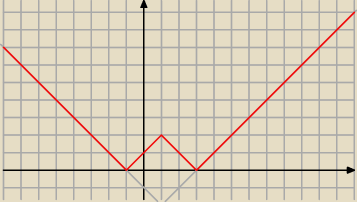na czerwono masz f(x) = | |x−1| − 2| Jak widzisz dla 2p−3 > 2 także będą tylko dwa rozwiązania

wredulus_pospolitus: 3)

3x		5		9x + 25
	+		=
5		3		15

	9x+25
i aby obie liczby były całkowite (czyli zarówno 'x' jak i		) to x musi być całkowite
	15

oraz 9x+25 musi być podzielne przez 15 (czyli przez 3 i przez 5) 9x ZAWSZE BĘDZIE PODZIELNE przez 3, a 25 nigdy ... więc 9x + 25 nigdy nie będzie podzielne przez 3 wniosek ...

Guest : Nigdy obie współrzędne nie będą całkowite

wredulus_pospolitus: co do (2) zauważ, że ... jeżeli najmniejszą z tych liczb naturalnych będzie 3 ... to suma odwrotności NIE DA Ci liczby naturalnej, bo:

1		1		1
	+		+		= 0.(3) + 0.25 + 0.2 < 0.85 < 1
3		4		5

jeżeli najmniejszą byłaby 2 ... to druga w kolejności musi być 3 ... bo inaczej:

1		1		1
	+		+		= 0.95 < 1
2		4		5

więc masz:

1		1		1
	+		+		= 1 <−−− wyznacz 'x'
2		3		x

uwaga ... a co by było gdyby najmniejszą liczbą była 1 ... wtedy niestety jakie byśmy nie dobrali dwie następne liczby naturalne to:

	1		1		1		1		1
1 <		+		+		≤ 1 +		+		< 2
	1		x		y		2		3

dlatego tylko to wcześniejsze równanie ma szansę spełniać warunki zadania

Guest : Dzięki wielkie