Planimetria Domestosus: Dwa okręgi przecinają się w punktach A i B. Przez punkt A poprowadzono sieczną przecinającą dane okręgi w punktach Ci D. Przez punkty Ci D poprowadzono styczne do danych okręgów, które przecięły się w punkcie E. Wykaż, że na czworokącie BCED można opisać okrąg

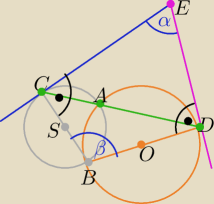
Eta: α+β=180^o wniosek ................. c.n.w.

Domestosus: Skąd wiadomo, że α + β = 180? W sensie znam twierdzenie tylko nie wiem jak udowodnić, że ich suma daje 180.

Domestosus: A w sumie nie ważne mamy dwa kąty proste, sorka za zamieszanie :v

Domestosus: Jeszcze raz dzięki za pomoc ^^

jc: Odcinki BC i BD nie muszą przechodzić przez środki okręgów, ale i tak prosta analiza kątów daje żądany wynik.

Eta: Jasne ,że nie muszą (tak mi się narysowało

jc: Ale wtedy kąty BCE i BDE nie nie będą proste.

Eta: Jasne jak "budowa ..."