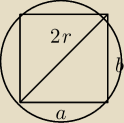
 Wśród wszystkich prostokątów o stałym polu S wskaż ten, na którym opisane koło ma najmniejsze
pole. Oblicz obwód tego prostokąta.
Moje rozwiązanie:
P=S=ab ⇒ b=S/a
Po = πr2
a∊(0;S)
z pitagorasa
4r2=S2/a2 + a2
i nwm co z tym dalej zrobić, w senie podstawiłem r2 do Po, ale nwm co z tym S w pochodnej
Wśród wszystkich prostokątów o stałym polu S wskaż ten, na którym opisane koło ma najmniejsze
pole. Oblicz obwód tego prostokąta.
Moje rozwiązanie:
P=S=ab ⇒ b=S/a
Po = πr2
a∊(0;S)
z pitagorasa
4r2=S2/a2 + a2
i nwm co z tym dalej zrobić, w senie podstawiłem r2 do Po, ale nwm co z tym S w pochodnej
| π*4r2 |
| |||||||||
f(r) = πr2 = | = π | = f(a) | ||||||||
| 4 | 4 |
