Dowód z okręgami LOL ALE PADAKA: Czworokąt ABCD podzielono przekątną AC na twa trójkąty. W trójkąty te wpisano okręgi. Wykaż, że okręgi te są styczne do AC w tym samym punkcie wtedy i tylko wtedy, gdy na czworokącie można opisać okrąg.

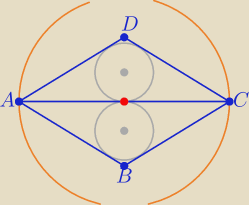
Eta: Nie da się udowodnić czegoś co nie jest prawdą ( masz na rys. przykład rombu

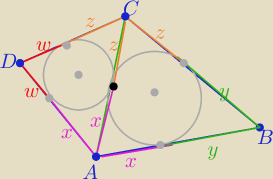
Eta: Myślę,że treść jest taka: " wtedy i tylko wtedy gdy w czworokąt można wpisać okrąg" 1/ tw. o odcinkach stycznych 2/ warunek wpisania okręgu w czworokąt w+x+z+y= x+y+z+w ( sumy długości przeciwległych boków są równe zatem w taki czworokąt da się wpisać okrąg

LOL ALE PADAKA: Rozwiązanie w podręczniku było właśnie takie jakby "wtedy i tylko wtedy gdy w czworokąt można wpisać okrąg" jednak w poleceniu było "można opisać okrąg". Czyli błąd druku w książce. Wszystko zrozumiałe! Dzięki wielkie