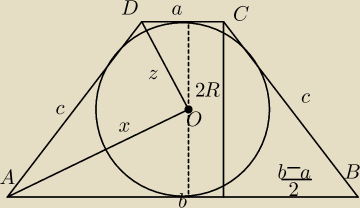
Pokaz ze Maciess: W trapez równoramienny ABCD wpisano okrąg o środku O. Pokaż, że średnia arytmetyczna długości podstaw trapezu ABCD jest równa √|OA|² + |OD|² . Intuicja podpowiada mi że trojkat ODA jest prostokątny. Próbowałem to wykazac z twierdzenia odwrotnego do twierdzenia do Pitagorasa ale cos nie wyszło Jakaś wskazówka z czego skorzystac? To ze a+b=2c to wiem.

wredulus_pospolitus: zauważ, że skoro mamy tutaj trapez opisany na okręgu to zachodzi: a+b = c+c

	a+b
więc c =
	2

i teraz tw. Pitagorasa i po sprawie

iteRacj@: Chyba bez ΔODA się nie da wykazać. Zaznacz pkt styczności na DA i z trójkątów podobnych wykaż kąt prosty.

iteRacj@: Chodzi mi o to, że skorzystać z Pitagorasa można dopiero, jak się pokaże że <DOA jest prosty.

Maciess:

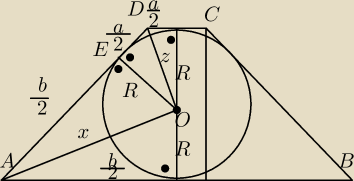
	a+b		b		a
|AD|=(a+b)/2 czyli |ED|=c−b/2=		−		=
	2		2		2

	a2		b2
z2=		+R2 x2=		+R2
	4		4

	(a+b)2		(a−b)2
c2=		i c2=4R2+
	4		4

(a+b)2		(a−b)2
	=4R2+
4		4

	(a+b)2		(a−b)2
4R2=		−
	4		4

4R²=ab

	ab
2R2=
	2

a2+b2

ab

(a+b)2

ab

(a+b)2

(2c)2

x2+z2=2R2+

=

+

−

=

=

=c2

4

2

4

2

4

4

czyli trojkat prostokątny Czy mozna jakos łatwiej?

iteRacj@: |<DAB|+|<ADC| =180^o //kąty przy podstawach trapezu

	1
|<DAO|=		|<DAB|
	2

	1
|<EDO|=		|<ADC| // środek okręgu wpisanego wyznaczyły dwusieczne kątów
	2

|<DAO|+|<EDO| =90^o w ΔDAO |<DAO|+|<EDO|+|<DOA|=90^o+|<DOA|=180^o |<DOA| =90^o

Mila:

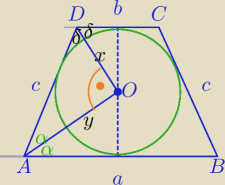
	a+b
1)a+b=2c⇔c=		− warunek z wpisania okręgu w czworokąt
	2

2) środek okręgu wpisanego w trapez leży w punkcie przecięcia dwusiecznych kątów ⇔ 2α+2δ=180⇔α+δ=90⇔ΔAOD− Δprostokątny 3) c²=x²+y²

	a+b
(		)2=|AO|2+|DO|2
	2

{a+b}{2}=√|AO|²+|DO|² cnw ================

Mila:

a+b
	=√|AO|2+|DO|2
2